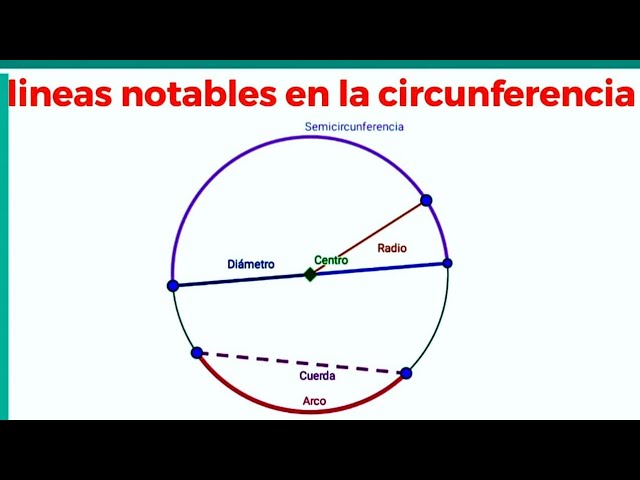
Las líneas notables de una circunferencia son elementos geométricos que se pueden trazar en relación con una circunferencia. Estas líneas tienen propiedades y características interesantes que nos ayudan a comprender mejor la geometría y las formas circulares.
¿Qué son las líneas notables?
Las líneas notables de una circunferencia son líneas o segmentos específicos que se pueden trazar a partir de una circunferencia. Estas líneas tienen propiedades matemáticas únicas y nos permiten explorar diferentes aspectos de las circunferencias y su geometría.
Diámetro
El diámetro es una de las líneas notables más básicas de una circunferencia. Se define como cualquier línea recta que pasa por el centro de la circunferencia y tiene sus extremos en la propia circunferencia. El diámetro es el segmento más largo que se puede trazar en una circunferencia y es exactamente el doble de la longitud del radio.
Radio
El radio es otra línea notable fundamental de una circunferencia. Se define como cualquier segmento que conecta el centro de la circunferencia con cualquier punto de la circunferencia en sí. El radio es siempre de la misma longitud para todos los puntos de una circunferencia, y es la mitad de la longitud del diámetro. El radio es una línea importante debido a su relación con el círculo y muchas de sus propiedades.
Cuerda
Una cuerda es una línea recta que conecta dos puntos de una circunferencia sin pasar por el centro. El segmento que une los extremos de la cuerda se llama arco. La cuerda tiene una longitud menor o igual a la del diámetro, dependiendo de la posición de los puntos en la circunferencia. Las cuerdas también pueden ser cuerda secante cuando atraviesan la circunferencia y cuerda tangente cuando solo tocan la circunferencia en un solo punto.
Tangente
Una tangente es una línea recta que toca una circunferencia en un solo punto, sin cruzarla. Esta línea es perpendicular al radio que conecta el centro de la circunferencia con el punto de contacto de la tangente. La tangente tiene una relación especial con la circunferencia y puede usarse para determinar ángulos, construir triángulos y resolver problemas geométricos.
Propiedades y aplicaciones de las líneas notables
Las líneas notables de una circunferencia tienen propiedades y aplicaciones interesantes en diferentes áreas de la geometría y las matemáticas. Vamos a explorar algunas de ellas:
Relación entre diámetro y radio
La relación entre el diámetro y el radio de una circunferencia es fundamental. El radio siempre es la mitad del diámetro, sin importar el tamaño de la circunferencia. Esta relación nos ayuda a comprender mejor la simetría y las proporciones de las circunferencias y los círculos.
Aplicación
Esta relación se mantiene constante en todas las circunferencias y se utiliza en muchas aplicaciones prácticas, como el diseño y la construcción de ruedas, engranajes y objetos redondos en general. Entender esta relación nos permite hacer cálculos precisos y crear objetos geométricamente equilibrados.
Longitud de una cuerda
La longitud de una cuerda depende de la posición de los puntos de conexión en la circunferencia. La cuerda será más larga si los puntos están más separados, y será igual al diámetro si los puntos están en los extremos del diámetro. Esta propiedad es útil para determinar la distancia entre dos puntos en una circunferencia y se aplica en múltiples áreas, como cartografía y diseño de ruedas dentadas.
Aplicación
En cartografía, la distancia entre dos puntos en un mapa se puede calcular usando la longitud de la cuerda entre los puntos correspondientes en la circunferencia que representa el área mapeada. Del mismo modo, en el diseño de ruedas dentadas, la longitud de la cuerda se utiliza para determinar la ubicación precisa de los dientes en el círculo correspondiente.
Ángulos y tangentes
Las tangentes son líneas que tocan una circunferencia en un solo punto y son perpendiculares al radio que conecta el centro con el punto de contacto. Estas líneas tienen una serie de propiedades y aplicaciones relacionadas con los ángulos.
Aplicación
Las tangentes se utilizan en trigonometría para calcular ángulos y resolver problemas relacionados con triángulos y formas geométricas. También se utilizan en física para describir la trayectoria de un objeto que se mueve en una circunferencia o una curva.
Las líneas notables de una circunferencia son elementos importantes en el estudio de la geometría y las formas circulares. El diámetro, el radio, las cuerdas y las tangentes tienen propiedades interesantes que nos ayudan a comprender mejor las circunferencias y aplicar estos conceptos en diversos campos.
Si bien hemos explorado solo algunas de las propiedades y aplicaciones de estas líneas notables, hay mucho más por descubrir y aprender. Las circunferencias y sus líneas notables son fundamentales en muchas áreas de las matemáticas y también tienen aplicaciones prácticas en el mundo real.
Si te gusta la geometría y quieres profundizar más en el estudio de las circunferencias y sus líneas notables, te invitamos a investigar más y descubrir todo lo que tienen para ofrecer. ¡La geometría es un mundo fascinante lleno de formas y patrones interesantes!
Aquí tienes algunas preguntas frecuentes sobre las líneas notables de una circunferencia:
¿Pueden las líneas notables de una circunferencia estar curvadas?
No, las líneas notables de una circunferencia son siempre líneas rectas. Estas líneas se pueden curvar o doblar solo si la circunferencia misma está curvada o deformada.
¿Existe alguna relación entre las cuerdas y las tangentes de una circunferencia?
Sí, las cuerdas y las tangentes tienen una relación interesante. Las cuerdas se pueden considerar como segmentos de una línea recta que conecta dos puntos en la circunferencia, mientras que las tangentes son líneas rectas que tocan la circunferencia en un solo punto. Las tangentes son siempre perpendiculares a los radios que conectan el centro con los puntos de contacto.
¿Las líneas notables de una circunferencia tienen algún uso práctico?
Sí, las líneas notables de una circunferencia tienen muchas aplicaciones prácticas en áreas como la ingeniería, la física, la cartografía, el diseño y la arquitectura. Estas líneas nos ayudan a comprender las formas y patrones circulares, y se utilizan en el diseño de ruedas, engranajes, circuitos eléctricos y mucho más.