1. Medida de los lados de un triángulo
El triángulo es una figura geométrica que consta de tres lados y tres ángulos. Para poder analizar o resolver problemas relacionados con triángulos, es importante tener en cuenta la medida de sus lados.
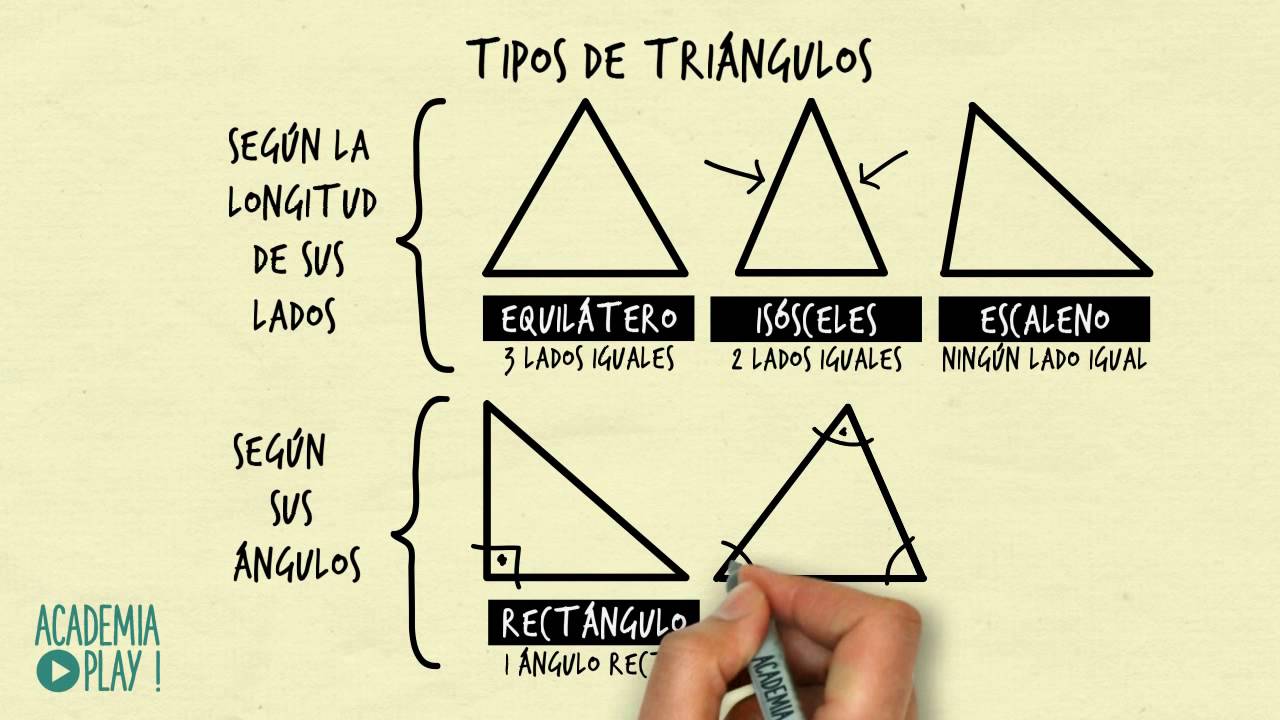
Existen diferentes formas de clasificar los triángulos según la medida de sus lados. A continuación, mencionaremos las tres clasificaciones más comunes:
Triángulo equilátero:
Un triángulo equilátero es aquel que tiene sus tres lados iguales. Esto implica que sus tres ángulos también serán iguales, y cada ángulo medirá 60 grados.
Triángulo isósceles:
Un triángulo isósceles es aquel que tiene dos lados iguales y uno distinto. Los dos ángulos opuestos a los lados iguales también serán iguales entre sí. El ángulo opuesto al lado distinto será distinto.
Triángulo escaleno:
Un triángulo escaleno es aquel que tiene los tres lados y los tres ángulos diferentes. No existe ninguna relación de igualdad entre sus lados ni entre sus ángulos.
Conocer la medida de los lados de un triángulo es fundamental para poder determinar su tipo y aplicar las propiedades y fórmulas correspondientes. Además, esta información también es necesaria para calcular su perímetro y área, entre otros cálculos.
2. Cálculo de los ángulos en un triángulo
En un triángulo, la suma de los ángulos interiores siempre es igual a 180 grados.
Existen diferentes métodos para calcular los ángulos en un triángulo, como la ley de los senos y la ley de los cosenos.
1. Ley de los senos:
Esta ley establece que en todo triángulo, la razón entre la medida de un lado y el seno del ángulo opuesto a ese lado, es constante.
La fórmula de la ley de los senos es: a / sin(A) = b / sin(B) = c / sin(C)
Donde “a”, “b” y “c” son las longitudes de los lados del triángulo, y “A”, “B” y “C” son los ángulos opuestos a cada uno de estos lados, respectivamente.
2. Ley de los cosenos:
Esta ley establece una relación entre los lados y los ángulos de un triángulo.
La fórmula de la ley de los cosenos es: a^2 = b^2 + c^2 – 2bc * cos(A)
Esta fórmula se puede aplicar para calcular la longitud de uno de los lados de un triángulo si se conocen las medidas de los otros dos lados y el ángulo opuesto al lado que se desea calcular.
Además, la ley de los cosenos también se puede utilizar para calcular los ángulos de un triángulo, utilizando la fórmula: cos(A) = (b^2 + c^2 – a^2) / 2bc
3. Suma de los ángulos interiores:
En todo triángulo, la suma de los ángulos interiores siempre es igual a 180 grados.
Esto significa que si conocemos la medida de dos de los ángulos interiores de un triángulo, podemos calcular el tercer ángulo restando la suma de los dos ángulos conocidos a 180 grados.
Por ejemplo, si conocemos que un triángulo tiene un ángulo de 60 grados y otro de 90 grados, podemos calcular el tercer ángulo de la siguiente manera: 180 – 60 – 90 = 30 grados.
Estos métodos son útiles para calcular los ángulos en un triángulo y resolver problemas geométricos relacionados con ellos.
3. Tipos de triángulos según sus lados
Existen diferentes tipos de triángulos según la longitud de sus lados. Estos son:
1. Triángulo equilátero:
Un triángulo equilátero es aquel que tiene sus tres lados de igual longitud. Todos los ángulos internos también son iguales, midiendo 60 grados cada uno.
2. Triángulo isósceles:
Un triángulo isósceles es aquel que tiene dos lados de igual longitud y uno diferente. Los ángulos opuestos a los lados iguales también son iguales.
3. Triángulo escaleno:
Un triángulo escaleno es aquel que tiene sus tres lados de longitudes diferentes. Todos los ángulos internos también son diferentes.
Estos son los principales tipos de triángulos según sus lados. Cada uno tiene características distintas y propiedades particulares.
4. Tipos de triángulos según sus ángulos
Los triángulos se clasifican según sus ángulos en tres tipos: triángulos acutángulos, triángulos obtusángulos y triángulos rectángulos. Esta clasificación se basa en la medida de los ángulos internos de cada triángulo.
Triángulos acutángulos
Un triángulo acutángulo es aquel que tiene todos sus ángulos internos agudos, es decir, menores a 90 grados. En este tipo de triángulo, la suma de los tres ángulos es siempre menor a 180 grados.
Triángulos obtusángulos
Un triángulo obtusángulo es aquel que tiene uno de sus ángulos internos obtuso, es decir, mayor a 90 grados. Los otros dos ángulos internos son agudos, es decir, menores a 90 grados. La suma de los tres ángulos de este tipo de triángulo siempre es mayor a 180 grados.
Triángulos rectángulos
Un triángulo rectángulo es aquel que tiene uno de sus ángulos internos recto, es decir, igual a 90 grados. Los otros dos ángulos internos son agudos, es decir, menores a 90 grados. La suma de los tres ángulos de este triángulo siempre es igual a 180 grados.
Es importante tener en cuenta estos tipos de triángulos según sus ángulos, ya que nos permiten entender y clasificar los diferentes triángulos que podemos encontrar en geometría.
5. Aplicaciones prácticas de la geometría del triángulo
La geometría del triángulo tiene numerosas aplicaciones prácticas en diversos campos, desde la arquitectura y la ingeniería hasta la física y la navegación. A continuación, se presentan algunas de las principales aplicaciones:
1. Construcción de edificios y estructuras
En la arquitectura y la ingeniería civil, la geometría del triángulo es fundamental para el diseño y la construcción de edificios y estructuras. El análisis de triángulos permite determinar dimensiones, ángulos y proporciones precisas, asegurando la estabilidad y resistencia de las construcciones.
2. Navegación marítima y aérea
En la navegación, los triángulos son utilizados para determinar posiciones y direcciones. La navegación marítima y aérea se basa en el uso de triángulos esféricos, conocidos como triángulos de posición, para calcular la ubicación de un objeto en relación con la posición del observador y otros puntos de referencia.
3. Topografía y cartografía
La topografía y la cartografía se apoyan en la geometría del triángulo para representar y medir el terreno y las áreas geográficas. Mediante el uso de técnicas triangulares, se pueden crear mapas detallados y realizar mediciones precisas de distancias, altitudes y pendientes.
4. Cálculos en trigonometría
La trigonometría, rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos, tiene múltiples aplicaciones prácticas. Se utiliza en campos como la física, la ingeniería, la navegación y la astronomía, para resolver problemas de cálculo de distancias, alturas, velocidades o ángulos.
5. Diseño gráfico y animación
En el ámbito del diseño gráfico y la animación, la geometría del triángulo es esencial para la creación de imágenes, formas y composiciones. Los triángulos son elementos fundamentales en el diseño de logotipos, ilustraciones y animaciones, permitiendo generar estructuras visuales equilibradas y atractivas.
Estas son solo algunas de las aplicaciones prácticas de la geometría del triángulo, pero su relevancia y utilidad se extienden a muchos otros campos, destacando su papel en la resolución de problemas geométricos y matemáticos en general.