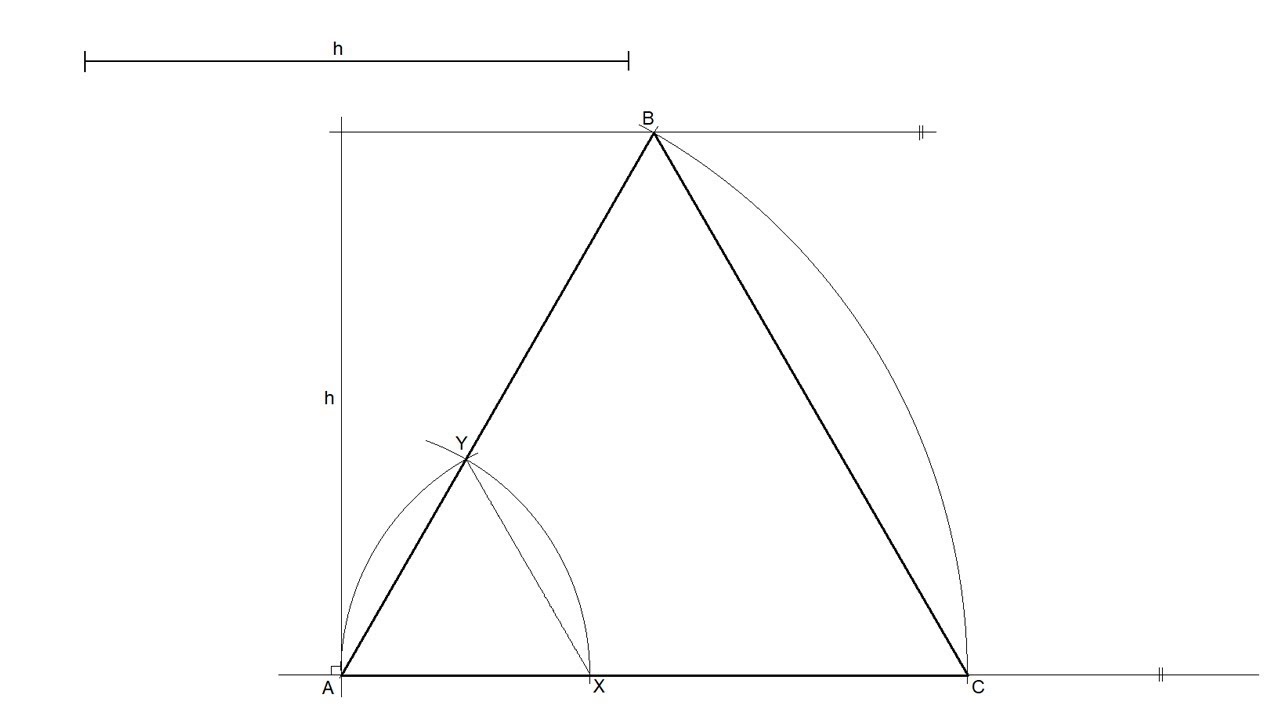
¿Qué es un triángulo equilátero?
Un triángulo equilátero es un tipo especial de triángulo en el cual todos sus lados son iguales. Esto significa que tiene tres ángulos internos de 60 grados cada uno.
La característica principal del triángulo equilátero es la igualdad de sus lados, lo cual lo diferencia de otros tipos de triángulos como el isósceles o el escaleno.
Al tener todos sus lados iguales, el triángulo equilátero también tiene todas sus alturas, medianas y bisectrices, que son líneas que dividen al triángulo en partes iguales, coincidiendo en un mismo punto.
Propiedades del triángulo equilátero:
- Todos los lados son iguales.
- Todos los ángulos internos miden 60 grados.
- Todas las alturas, medianas y bisectrices coinciden en un mismo punto.
- Tiene tres ejes de simetría.
- Puede ser inscrito en una circunferencia.
El triángulo equilátero es utilizado en diversas áreas de la geometría y la trigonometría, así como en la construcción de edificaciones y en la resolución de problemas matemáticos. Su forma regular y simétrica lo hace fácil de trabajar y analizar.
En resumen, un triángulo equilátero es aquel en el que todos sus lados son iguales y sus ángulos internos miden 60 grados. Esta figura geométrica posee propiedades especiales y es ampliamente utilizada en diferentes campos.
Fórmula para calcular el área de un triángulo equilátero con altura conocida
Un triángulo equilátero es aquel que tiene todos sus lados iguales y todos sus ángulos internos de 60 grados. Para calcular su área, necesitamos conocer la altura del triángulo.
Paso 1: Calcular la longitud de un lado del triángulo
Para encontrar la longitud de un lado del triángulo, podemos utilizar el teorema de Pitágoras. Si conocemos la altura, podemos dividir el triángulo en dos triángulos rectángulos y utilizar la siguiente fórmula:
a = (altura del triángulo) / √3
Paso 2: Calcular el área del triángulo
Una vez que conocemos la longitud de un lado del triángulo, podemos calcular su área utilizando la siguiente fórmula:
Área = (lado del triángulo) * (altura del triángulo) / 2
Por lo tanto, el área de un triángulo equilátero con altura conocida se puede calcular multiplicando la longitud de un lado del triángulo por la altura del triángulo y dividiendo el resultado entre 2.
Procedimiento paso a paso para calcular el área de un triángulo equilátero con altura conocida
¡Hola a todos!
En esta ocasión, les mostraremos un procedimiento paso a paso para calcular el área de un triángulo equilátero con altura conocida. ¡Espero que les sea de utilidad!
Paso 1: Conocer la fórmula para calcular el área de un triángulo equilátero
El área de un triángulo equilátero puede ser calculada con la siguiente fórmula:
Área = (lado^2 * √3) / 4
Donde “lado” representa la longitud de uno de los lados del triángulo equilátero.
Paso 2: Obtener el valor de la altura del triángulo
En este caso, se nos proporciona la altura del triángulo. Por lo tanto, no es necesario realizar ningún cálculo adicional para obtener su valor.
Paso 3: Calcular la longitud de uno de los lados del triángulo equilátero
Para calcular la longitud de uno de los lados del triángulo equilátero, utilizamos la siguiente fórmula:
Lado = (2 * altura) / √3
Donde “altura” representa el valor conocido de la altura del triángulo.
Paso 4: Sustituir los valores en la fórmula del área
Ahora que conocemos el valor de “lado”, podemos sustituirlo en la fórmula del área para obtener el resultado deseado.
Área = (lado^2 * √3) / 4
Recordemos que “lado” representa la longitud de uno de los lados calculada anteriormente.
Paso 5: Resolver la fórmula y obtener el área del triángulo
Una vez que hemos sustituido los valores correspondientes, procedemos a realizar las operaciones matemáticas para obtener el área del triángulo equilátero.
Recuerden que la operación “^2” significa elevar al cuadrado y “√” representa la raíz cuadrada.
¡Y eso es todo! Ahora conocemos el procedimiento paso a paso para calcular el área de un triángulo equilátero con altura conocida. Espero que les haya resultado útil y que puedan aplicarlo en sus propios cálculos. ¡Hasta la próxima!
Ejemplo numérico
En este post, vamos a explorar un ejemplo numérico utilizando etiquetas HTML para resaltar las frases más importantes del texto.
Supongamos que tenemos una lista de calificaciones de un examen y queremos calcular el promedio. Las calificaciones son las siguientes:
- Calificación 1: 90
- Calificación 2: 85
- Calificación 3: 95
- Calificación 4: 88
- Calificación 5: 92
Para obtener el promedio, simplemente sumamos todas las calificaciones y las dividimos entre la cantidad de calificaciones. En este caso, tenemos 5 calificaciones.
Suma de calificaciones: 90 + 85 + 95 + 88 + 92 = 450
Promedio: 450 / 5 = 90
Entonces, el promedio de las calificaciones es 90.
Podemos utilizar etiquetas HTML para resaltar las frases más importantes en este ejemplo. Por ejemplo, utilizamos la etiqueta <strong> para resaltar las calificaciones y los valores importantes en las operaciones matemáticas.
En resumen, mediante el uso de etiquetas HTML como listas, <strong> y <b>, podemos resaltar información clave en nuestro texto y hacer que sea más fácil de entender y seguir.
Usos y aplicaciones del triángulo equilátero con altura conocida
El triángulo equilátero con altura conocida es un caso especial de triángulo que tiene muchas aplicaciones en diversos campos. En este artículo, exploraremos algunos de los usos más comunes de este tipo de triángulo.
1. Construcción de estructuras
El triángulo equilátero con altura conocida es ampliamente utilizado en la construcción de estructuras debido a su estabilidad y simetría. Por ejemplo, en arquitectura, se utiliza para calcular la altura y ubicación de los techos, especialmente en edificios con forma triangular.
2. Cálculo de áreas
Otro uso común del triángulo equilátero con altura conocida es en el cálculo de áreas. Las fórmulas matemáticas para calcular el área de un triángulo equilátero requieren el uso de su altura conocida. Esta información es útil en campos como la geometría, la física y la ingeniería.
3. Diseño de gráficos y logotipos
En el diseño gráfico y la creación de logotipos, el triángulo equilátero con altura conocida es utilizado para dar una apariencia equilibrada y simétrica a las imágenes. Su forma geométrica y proporciones simétricas se consideran estéticamente agradables y atractivas visualmente.
4. Análisis de fuerzas
En el campo de la ingeniería estructural, el triángulo equilátero con altura conocida se utiliza en el análisis de fuerzas y cargas. Esta forma de triángulo es especialmente útil para determinar la distribución de fuerzas en puentes, torres y otras estructuras.
En resumen, el triángulo equilátero con altura conocida tiene diversos usos y aplicaciones en diferentes campos. Desde la construcción de estructuras hasta el diseño gráfico y el análisis de fuerzas, su simetría y estabilidad lo convierten en una forma geométrica invaluable. ¡Aprovecha las ventajas de este tipo de triángulo en tus proyectos!