Encabezado del segundo párrafo: ¿Qué es el apotema de un pentágono y por qué es importante?
¡Hola, querido lector! En este artículo te llevaré en un emocionante viaje matemático para aprender cómo calcular el apotema de un pentágono. Pero, antes de sumergirnos en los cálculos, es importante entender qué es el apotema y por qué es relevante en la geometría.
¿Qué es el apotema de un polígono?
Antes de hablar específicamente del apotema del pentágono, es necesario comprender el concepto de apotema en general. En geometría, el apotema se refiere a la distancia más corta entre el centro de un polígono regular y uno de sus lados. En otras palabras, es la distancia desde el centro del polígono hasta el punto medio de uno de sus lados.
El apotema es especialmente útil para calcular el área de los polígonos regulares, ya que nos permite encontrar la longitud de los lados y aplicar fórmulas específicas para determinar el área total. Además, el apotema es esencial para otros cálculos geométricos, como el perímetro, el radio y la circunferencia.
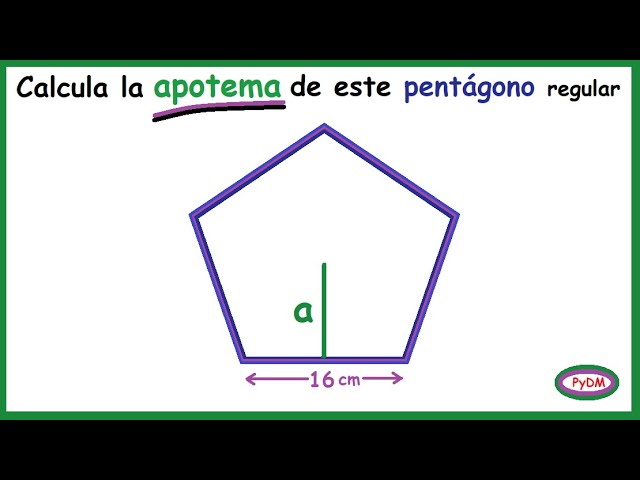
¿Cómo calcular el apotema de un pentágono?
Ahora que conocemos la importancia del apotema, veamos cómo calcularlo específicamente para un pentágono. Un pentágono es un polígono de cinco lados iguales y cinco ángulos iguales, y para encontrar su apotema necesitamos conocer la longitud de uno de sus lados.
Para calcular el apotema de un pentágono, podemos utilizar la siguiente fórmula:
apotema = lado / (2 * tan(180° / número de lados))
Donde «lado» es la longitud de uno de los lados del pentágono y «número de lados» es 5 en el caso de un pentágono. La fórmula hace uso de la función trigonométrica tangente (tan) para determinar el apotema.
Por ejemplo, si tenemos un pentágono con un lado de longitud 8 cm, podemos calcular su apotema de la siguiente manera:
apotema = 8 / (2 * tan(180° / 5))
apotema ≈ 8 / (2 * tan(36°))
apotema ≈ 8 / (2 * 0.726542528)
apotema ≈ 8 / 1.453085056
apotema ≈ 5.507463633 cm
¡Y ahí lo tienes! El apotema de nuestro pentágono sería aproximadamente 5.5 cm.
Aplicaciones prácticas del apotema del pentágono
Comprender cómo calcular el apotema de un pentágono puede tener varias aplicaciones prácticas en el mundo real. A continuación, te presento algunas de ellas:
Construcción de edificios y estructuras
En arquitectura, el apotema se utiliza para calcular la distancia desde el centro de un polígono regular hasta su lado, lo que permite determinar con precisión las dimensiones de los diferentes elementos de una estructura. Por ejemplo, al construir una cúpula en forma de pentágono, el apotema es esencial para establecer el tamaño correcto de los segmentos y los ángulos necesarios para su construcción.
Diseño de objetos y arte
En el diseño industrial y el arte, el apotema se utiliza para crear formas regulares y simétricas. Conocer el apotema de un pentágono puede ser útil para diseñar objetos decorativos, como lámparas, jarrones o esculturas, y lograr proporciones armónicas y estéticamente agradables.
Cálculos de áreas y volúmenes
El apotema es una parte integral en la fórmula para calcular el área de un pentágono regular. Conocer el apotema nos permite determinar con precisión la superficie de un pentágono en relación a su base. Además, cuando el pentágono se extrude, el apotema es esencial para calcular el volumen resultante de la figura tridimensional.
Problemas de geometría y matemáticas avanzadas
El apotema del pentágono también puede ser requerido en problemas de geometría y matemáticas avanzadas, especialmente cuando se trata de calcular áreas o perímetros de formas irregulares. Dominar el cálculo del apotema nos proporciona una herramienta más en nuestro arsenal para enfrentar desafíos matemáticos y resolverlos de manera efectiva.
Para finalizar este artículo, responderé algunas preguntas frecuentes que pueden surgir al explorar el cálculo del apotema en un pentágono:
¿El apotema siempre es más corto que el lado de un pentágono?
Sí, el apotema siempre será más corto que el lado de un pentágono regular. Esto se debe a que la distancia más corta entre el centro del pentágono y uno de sus lados siempre será menor que la longitud completa de dicho lado. El apotema actúa como una línea diagonal interna del pentágono, conectando su centro con uno de los vértices.
¿Qué sucede si el pentágono es irregular?
El cálculo del apotema en pentágonos irregulares puede volverse más complejo, ya que los lados ya no son todos iguales. Sin embargo, en muchos casos, puedes considerar el pentágono irregular como una combinación de triángulos y cuadriláteros regulares, y calcular el apotema para cada uno de ellos. Luego, puedes encontrar un promedio ponderado de los apotemas individuales para obtener una estimación del apotema total del pentágono irregular.
¿Hay alguna forma más fácil de calcular el apotema de un pentágono?
Si conoces el radio de la circunferencia circunscrita al pentágono, también puedes calcular el apotema usando la fórmula:
apotema = radio * cos(180° / número de lados)
Esta fórmula se deriva de la relación entre el radio, el apotema y la apotema del triángulo rectángulo formado por la mitad de un lado del pentágono, el apotema y el radio de la circunferencia circunscrita.
Y con eso, llegamos al final de nuestro viaje a través del cálculo del apotema del pentágono. Espero que hayas disfrutado de este recorrido matemático y que hayas aprendido algo nuevo y emocionante. Explora las aplicaciones prácticas del apotema y desafíate a ti mismo con problemas geométricos. ¡Recuerda que las matemáticas están en todas partes y son fascinantes!
Si tienes alguna otra pregunta o algún comentario adicional, ¡no dudes en dejarlo en la sección de comentarios a continuación! Estaré encantado de responder a tus inquietudes y de continuar la conversación. ¡Hasta la próxima aventura matemática!
.formula {
background-color: #f2f2f2;
padding: 10px;
font-family: monospace;
}