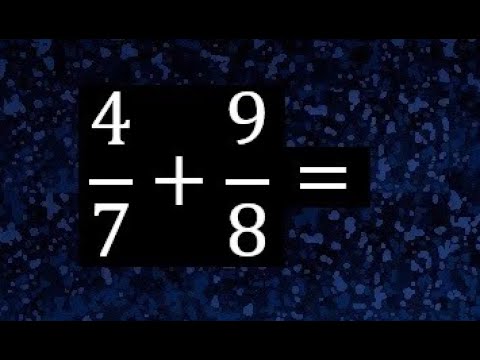¿Qué relación tienen los números entre 9/8 y 7/4?
En matemáticas, es común encontrarnos con números fraccionarios o racionales. Estos números expresan una relación o proporción entre dos cantidades y pueden tener valores más complejos. En este artículo, exploraremos la relación entre los números comprendidos entre 9/8 y 7/4, y cómo estos números tienen un rango específico y fascinante en el mundo de las matemáticas.
¿Qué es un número racional?
Antes de sumergirnos en el tema principal, es importante comprender qué es un número racional. Un número racional es aquel que puede ser expresado como una fracción, donde el numerador y el denominador son números enteros. Esto incluye tanto los números enteros como los números decimales que se pueden convertir en fracciones. Por lo tanto, los números entre 9/8 y 7/4 son un tipo de número racional.
El rango de números entre 9/8 y 7/4
Los números entre 9/8 y 7/4 conforman un rango específico en el sistema de números racionales. Para visualizar mejor este rango, podemos convertir ambos extremos a números decimales. 9/8 es igual a 1.125 y 7/4 es igual a 1.75. Por lo tanto, todos los números entre 1.125 y 1.75 forman parte de este rango.
Es importante destacar que los números comprendidos en este rango no incluyen los extremos 1.125 y 1.75; van desde el número más cercano a 1.125 hasta el número más cercano a 1.75.
Patrones y propiedades en los números del rango
Al examinar los números dentro del rango entre 9/8 y 7/4, podemos observar ciertos patrones y propiedades que los hacen interesantes. A continuación, exploraremos algunos de ellos:
1. Patrón de aumento gradual
Una propiedad notable de los números en este rango es que aumentan gradualmente a medida que nos acercamos a 1.75. Si comenzamos desde 1.125 y vamos incrementando la cantidad en pequeños pasos, notaremos cómo los números se vuelven cada vez más cercanos a 1.75. Esto crea un patrón ascendente que refleja la naturaleza gradual de estos números.
2. Relación entre numerador y denominador
Al convertir los números del rango a fracciones, podemos observar la relación entre el numerador y el denominador. Por ejemplo, si tenemos el número 1.5 dentro del rango, podemos escribirlo como 3/2. Al examinar las fracciones dentro de este rango, es evidente que los numeradores son múltiplos de 3 y los denominadores son múltiplos de 2. Esta relación proporciona una conexión clave entre los números y muestra cómo están intrínsecamente relacionados entre sí.
3. Fracciones equivalentes
Otra propiedad interesante de los números dentro de este rango es que muchas de las fracciones son equivalentes. Esto significa que representan la misma cantidad, aunque se expresen de manera diferente. Por ejemplo, 3/2 es equivalentes a 6/4, ya que ambas representan la misma proporción en términos de media. Esta propiedad brinda una perspectiva fascinante sobre la versatilidad y la relación intrincada de los números racionales.
Conclusiones
En resumen, los números entre 9/8 y 7/4 pertenecen al rango específico de los números racionales. Estos números comparten propiedades y patrones interesantes, como el aumento gradual, la relación entre numerador y denominador, y la existencia de fracciones equivalentes. Explorar y comprender este rango de números contribuye a una apreciación más profunda de las matemáticas y muestra cómo los números no son solo símbolos, sino también entidades complejas e interconectadas.
Preguntas frecuentes
1. ¿Cómo se puede aplicar el conocimiento sobre los números entre 9/8 y 7/4 en la vida cotidiana?
Los números racionales, incluidos los que pertenecen a este rango específico, tienen aplicaciones en diversas áreas de la vida cotidiana. Por ejemplo, pueden ser útiles en situaciones que involucran proporciones, como recetas de cocina o mezclas de ingredientes. También son relevantes en finanzas, para calcular intereses y porcentajes. Comprender estos números puede mejorar nuestras habilidades matemáticas en la vida diaria.
2. ¿Cuál es la importancia de los números racionales en las matemáticas?
Los números racionales desempeñan un papel fundamental en las matemáticas, ya que permiten representar y operar con una amplia gama de valores. Estos números proporcionan una herramienta invaluable para medir, comparar y relacionar cantidades. Además, son la base de los números decimales y facilitan el cálculo y la resolución de problemas en diversos campos, desde la geometría hasta la física y la economía.
3. ¿Pueden los números irracionales existir entre 9/8 y 7/4?
No, los números irracionales no pueden existir entre 9/8 y 7/4, ya que los números irracionales son aquellos que no pueden ser expresados como una fracción o una proporción simple. Los números dentro de este rango son todos racionales, lo que significa que pueden expresarse como una fracción. Los números irracionales, como la raíz cuadrada de 2 o pi, no pueden ser representados exactamente con una fracción.
Espero que este artículo te haya brindado una comprensión más profunda de los números entre 9/8 y 7/4 y su importancia en el mundo de las matemáticas. Si tienes alguna otra pregunta relacionada con este tema, ¡no dudes en dejármela en los comentarios!