El decágono es una figura geométrica formada por diez lados y diez ángulos. En este artículo, exploraremos la medida de los ángulos internos de un decágono y cómo se pueden calcular. Además, discutiremos algunas propiedades interesantes de esta figura.
¿Qué es un decágono?
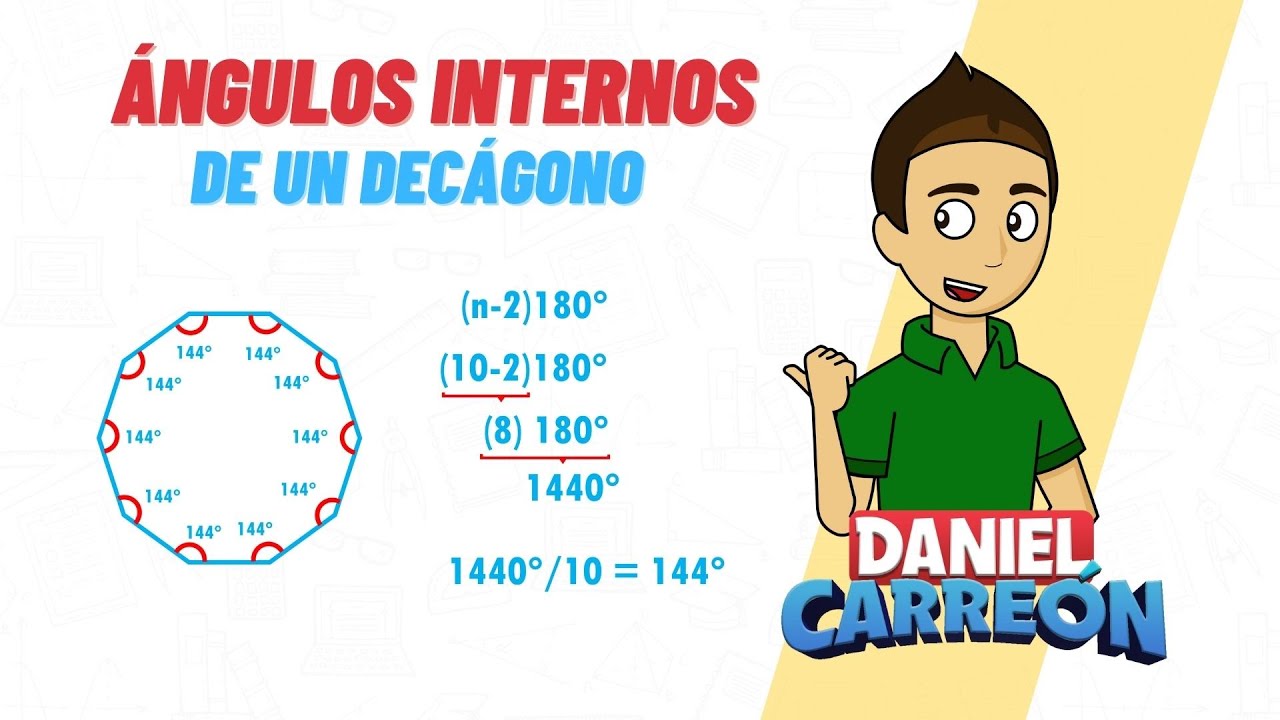
Un decágono es un polígono con diez lados y diez ángulos internos. Cada lado del decágono se conecta con el siguiente lado, formando una figura cerrada. Los ángulos internos de un decágono se encuentran dentro de la figura y tienen una suma total de 1440 grados.
Calcular la medida de los ángulos internos
Para calcular la medida de los ángulos internos de un decágono, se puede utilizar la fórmula:
Medida de cada ángulo interno = (n-2) * 180° / n
Donde «n» es el número de lados del polígono, en este caso, 10. Sustituyendo el valor de «n» en la fórmula, obtenemos:
Medida de cada ángulo interno = (10-2) * 180° / 10 = 144°
Por lo tanto, la medida de cada ángulo interno de un decágono es de 144 grados.
Propiedades del decágono
Además de la medida de los ángulos internos, el decágono tiene otras propiedades interesantes que vale la pena explorar. Algunas de ellas son:
Simetría de rotación
El decágono tiene una simetría de rotación de 36 grados. Esto significa que al rotar la figura 36 grados alrededor de su centro, se obtiene la misma figura original. Esta propiedad de simetría puede ser visualmente atractiva y se encuentra en muchas formas naturales y artificiales.
Suma de lados
La suma de los lados de un decágono es igual al perímetro de la figura. Para calcular el perímetro de un decágono, se suma la longitud de cada uno de sus diez lados. Esta propiedad es útil en aplicaciones prácticas, como calcular el material necesario para construir un decágono regular.
Polígono regular
Un decágono regular es un tipo especial de decágono en el que todos los lados tienen la misma longitud y todos los ángulos son congruentes. Esto significa que cada lado del decágono tiene la misma medida y cada ángulo interno también tiene la misma medida de 144 grados.
Aplicaciones del decágono
Aunque el decágono no es una figura geométrica tan común como el cuadrado o el triángulo, tiene algunas aplicaciones interesantes en el mundo real. Algunas de estas aplicaciones incluyen:
Arquitectura
En arquitectura, el decágono se ha utilizado en la construcción de edificios y estructuras para agregar un aspecto único y llamativo. Su simetría de rotación y propiedades estéticas lo convierten en una opción atractiva para diseñadores y arquitectos que buscan crear algo distintivo.
Jardinería
En el diseño de jardines, el decágono regular se ha utilizado como forma para arreglos de flores y plantas. La simetría y la estructura del decágono pueden crear patrones visualmente agradables y equilibrados en un jardín.
Geometría fractal
El decágono también se ha utilizado en el campo de la geometría fractal. Los fractales son patrones geométricos que se repiten a diferentes escalas. Al aplicar la simetría y las propiedades del decágono a fractales, se pueden crear estructuras complejas y visualmente atractivas.
¿Cuántos ángulos tiene un decágono?
Un decágono tiene un total de diez ángulos internos.
¿Cuál es la suma de los ángulos internos de un decágono?
La suma de los ángulos internos de un decágono es de 1440 grados.
¿Cuál es la medida de cada ángulo interno de un decágono?
La medida de cada ángulo interno de un decágono es de 144 grados.
¿Cuál es la diferencia entre un decágono regular y uno irregular?
Un decágono regular es aquel en el que todos los lados y ángulos son congruentes, es decir, tienen la misma medida. Un decágono irregular no cumple con esta condición y puede tener lados y ángulos de diferentes longitudes y medidas.
¿Cuáles son algunas aplicaciones prácticas del decágono?
El decágono se ha utilizado en arquitectura, diseño de jardines y geometría fractal, entre otras aplicaciones prácticas.
¿Por qué el decágono es una figura geométrica interesante?
El decágono es una figura geométrica interesante debido a sus propiedades de simetría, la medida constante de sus ángulos internos y sus posibles aplicaciones prácticas en diversos campos.
¿Cuál es la relación entre la medida de los ángulos internos y el número de lados en un polígono?
La relación entre la medida de los ángulos internos y el número de lados en un polígono se puede calcular utilizando la fórmula mencionada anteriormente: medida de cada ángulo interno = (n-2) * 180° / n.
¿Cuál es la importancia de comprender las propiedades de las figuras geométricas?
Comprender las propiedades de las figuras geométricas es importante en áreas como la resolución de problemas matemáticos, el diseño arquitectónico y la ingeniería, donde el conocimiento de las formas y sus propiedades puede ser fundamental para lograr resultados precisos y eficientes.