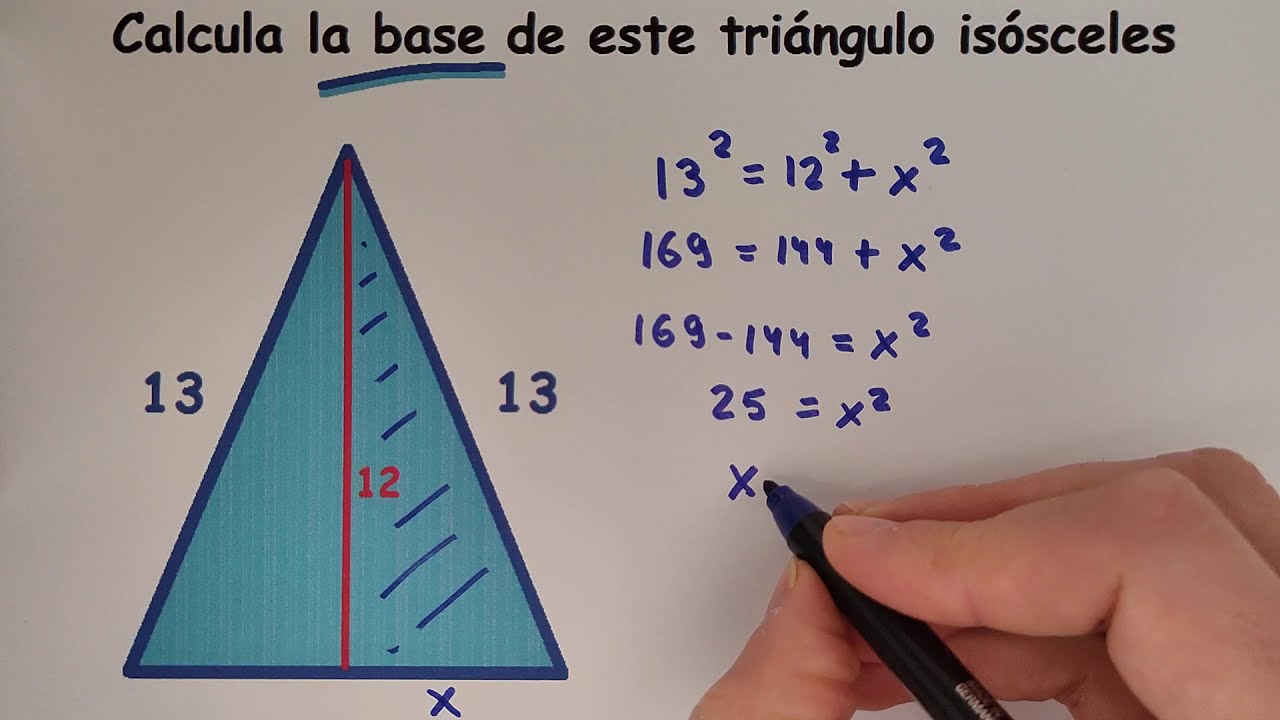
¿Qué es un triángulo isósceles?
Un triángulo isósceles es un tipo de triángulo que tiene dos lados iguales y dos ángulos iguales. Estos lados iguales se llaman lados de base y el ángulo opuesto a la base se conoce como el ángulo de vértice. La base puede ser cualquier lado del triángulo, pero generalmente se toma el lado más largo como la base.
¿Por qué es importante conocer la base de un triángulo isósceles?
Saber cómo encontrar la base de un triángulo isósceles es útil en muchos problemas y situaciones geométricas. La base puede ser necesaria para calcular el área del triángulo o para determinar la altura de un triángulo isósceles. Además, conocer la base nos permite identificar y clasificar adecuadamente el triángulo.
Paso 1: Identifica los lados y ángulos del triángulo isósceles
Antes de poder encontrar la base de un triángulo isósceles, primero debes identificar los lados y ángulos del triángulo. Recuerda que un triángulo isósceles tiene dos lados iguales y dos ángulos iguales. Puedes etiquetar los lados y ángulos para facilitar tu trabajo.
Paso 2: Utiliza el teorema de Pitágoras
Si conoces la longitud de los dos lados iguales y quieres encontrar la base, puedes utilizar el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.
Teorema de Pitágoras: a² = b² + c²
Donde “a” es la hipotenusa (la base en nuestro caso), y “b” y “c” son los otros dos lados del triángulo.
Paso 3: Aplica la fórmula para encontrar la base
Para encontrar la base de un triángulo isósceles, podemos reorganizar el teorema de Pitágoras para resolver la ecuación en términos de “a”, que es la base que estamos buscando.
Sustituyendo b = c:
a² = b² + b²
a² = 2b²
a = √(2b²)
Al aplicar esta fórmula, podemos encontrar la longitud de la base del triángulo isósceles.
Ejemplo práctico: Cálculo de la base
Supongamos que tenemos un triángulo isósceles con los lados iguales midiendo 5 cm cada uno. Queremos encontrar la longitud de la base.
Usando la fórmula que hemos mencionado anteriormente, podemos calcular la longitud de la base así:
a = √(2 * 5²)
a = √(2 * 25)
a = √50
a ≈ 7.07 cm
Entonces, la base de este triángulo isósceles es de aproximadamente 7.07 cm.
Preguntas frecuentes sobre la base de un triángulo isósceles
1. ¿Puedo encontrar la base si solo conozco la altura y un ángulo?
Sí, si conoces la altura y un ángulo del triángulo isósceles, puedes usar trigonometría para encontrar la base. Puedes utilizar las funciones trigonométricas seno, coseno o tangente, dependiendo de la información que tengas.
2. ¿Es posible tener una base más larga que los lados iguales en un triángulo isósceles?
No, en un triángulo isósceles, la base siempre es igual o más corta que los lados iguales. Si la base fuera más larga que los lados iguales, dejaría de ser un triángulo isósceles y se convertiría en un triángulo escaleno.
3. ¿Puedo encontrar la base si solo conozco el área del triángulo?
Sí, si conoces el área del triángulo isósceles, puedes utilizar la fórmula del área (base por altura dividido por 2) para encontrar la base. Simplemente despeja la base de la fórmula y sustituye los valores conocidos para resolverla.
4. ¿Es posible tener un triángulo isósceles con una base perpendicular a la altura?
No, en un triángulo isósceles, la base no puede ser perpendicular a la altura. Un triángulo con una base perpendicular a la altura es un triángulo rectángulo, no un triángulo isósceles.
5. ¿Cuál es la relación entre el ángulo de vértice y la base de un triángulo isósceles?
En un triángulo isósceles, el ángulo de vértice (el ángulo opuesto a la base) siempre es igual. Esto significa que si conoces el ángulo de vértice, puedes deducir que los ángulos de base también son iguales.