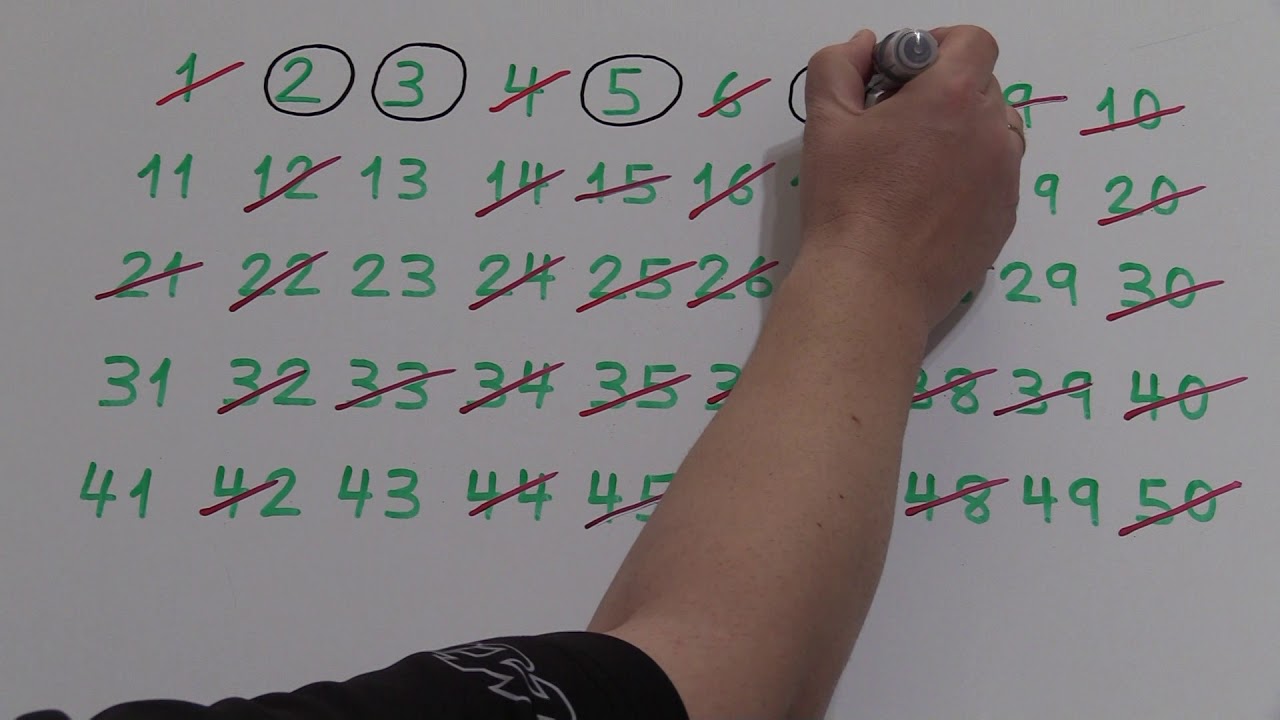¿Qué es un número primo?
Un número primo es aquel número mayor que 1 y que solo puede ser divisible por 1 y por sí mismo, sin tener más divisores. Es una propiedad que hace a los números primos algo especial, ya que no pueden ser escritos como el producto de otros números. En otras palabras, son números bien exclusivos.
Los primeros números primos
Si nos adentramos en el mundo de los números primos, encontraremos que el número 2 es el único número primo par. A partir de allí, los números primos comienzan a mostrarnos sus peculiaridades. A medida que avanzamos en la secuencia numérica, nos encontramos con el famoso número primo 3.
Es importante mencionar que el 1 no se considera un número primo, ya que no cumple con la definición de tener solo dos divisores.
Buscando el número primo de 50
En nuestro caso, estamos interesados en descubrir el número primo de 50. ¿Existirá un número primo en esta posición de la secuencia?
Comencemos por listar todos los números entre 1 y 50, excluyendo el número 1, ya que como mencionamos antes, no es considerado primo.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50
Observamos que en esta lista hay varios números que no cumplen con la propiedad de ser primos, como por ejemplo los múltiplos de 2 (4, 6, 8, etc.) o los múltiplos de 3 (9, 12, 15, etc.). Estos números ya los podemos descartar.
Si continuamos evaluando los números de la lista, veremos que el número 5 es primo, ya que no es divisible por ningún número diferente de 1 y de sí mismo. Por lo tanto, el número primo de la posición 50 es el 47.
Descifrando el patrón de los números primos
La búsqueda de números primos ha sido una fascinante tarea para matemáticos a lo largo de la historia. Aunque pareciera que no hay un patrón claro para la aparición de números primos en la secuencia numérica, existen teorías y patrones parciales que nos ayudan a comprender mejor su comportamiento.
Una de estas teorías es conocida como la conjetura de los números primos gemelos, que establece que existen infinitos pares de números primos consecutivos cuya diferencia es 2. Por ejemplo, 3 y 5 son números primos consecutivos y su diferencia es 2. Otro ejemplo es 11 y 13.
Esta conjetura nos muestra que, a medida que avanzamos en la secuencia numérica, es probable encontrar números primos que están cerca entre sí. Sin embargo, aún no se ha demostrado de manera definitiva esta conjetura y su verificación es un tema abierto en la matemática.
La importancia de los números primos
Aunque pareciera que los números primos son solo elementos curiosos dentro de las matemáticas, su importancia va más allá de lo académico. Estos números tienen aplicaciones en muchos campos, como la criptografía, el diseño de algoritmos, la teoría de números y la seguridad informática.
Por ejemplo, en criptografía se utilizan los números primos para generar claves de encriptación seguras. La dificultad de factorizar un número grande en sus factores primos es lo que hace que este tipo de sistemas sean seguros, ya que requiere un esfuerzo computacional inmenso.
Además, la teoría de números, que estudia las propiedades de los números enteros, tiene en los números primos una de sus ramas más importantes. La conjetura de Riemann, que está relacionada con la distribución de los números primos, es considerada uno de los problemas más difíciles sin resolver en matemáticas.
Preguntas frecuentes sobre los números primos
1. ¿El número 1 es primo?
No, el número 1 no se considera un número primo. La definición de números primos establece que deben ser mayores que 1 y solo tener dos divisores, lo cual no se cumple en el caso del número 1.
2. ¿Cuál es el número primo más grande conocido?
Hasta el momento, el número primo más grande conocido es el número primo de Mersenne M82589933, descubierto en 2018. Este número tiene 24,862,048 dígitos en su representación decimal.
3. ¿Existen números primos infinitos?
Sí, la infinitud de los números primos fue demostrada por el matemático Euclides en su obra “Los Elementos”, escrita alrededor del año 300 a.C. Aunque no se han encontrado todos los números primos posibles, se ha demostrado que la cantidad de números primos es infinita y que siempre se podrán encontrar nuevos números primos.
En conclusión, los números primos son elementos fascinantes dentro del mundo de las matemáticas. Aunque descubrir el número primo de una posición específica en la secuencia numérica puede ser un desafío, es un campo de estudio apasionante que tiene aplicaciones en diversos ámbitos. Desde la criptografía hasta la teoría de números, los números primos nos invitan a explorar y comprender mejor las propiedades de los números y su comportamiento en el universo matemático. ¿Cuál será el próximo descubrimiento o desafío en el mundo de los números primos?