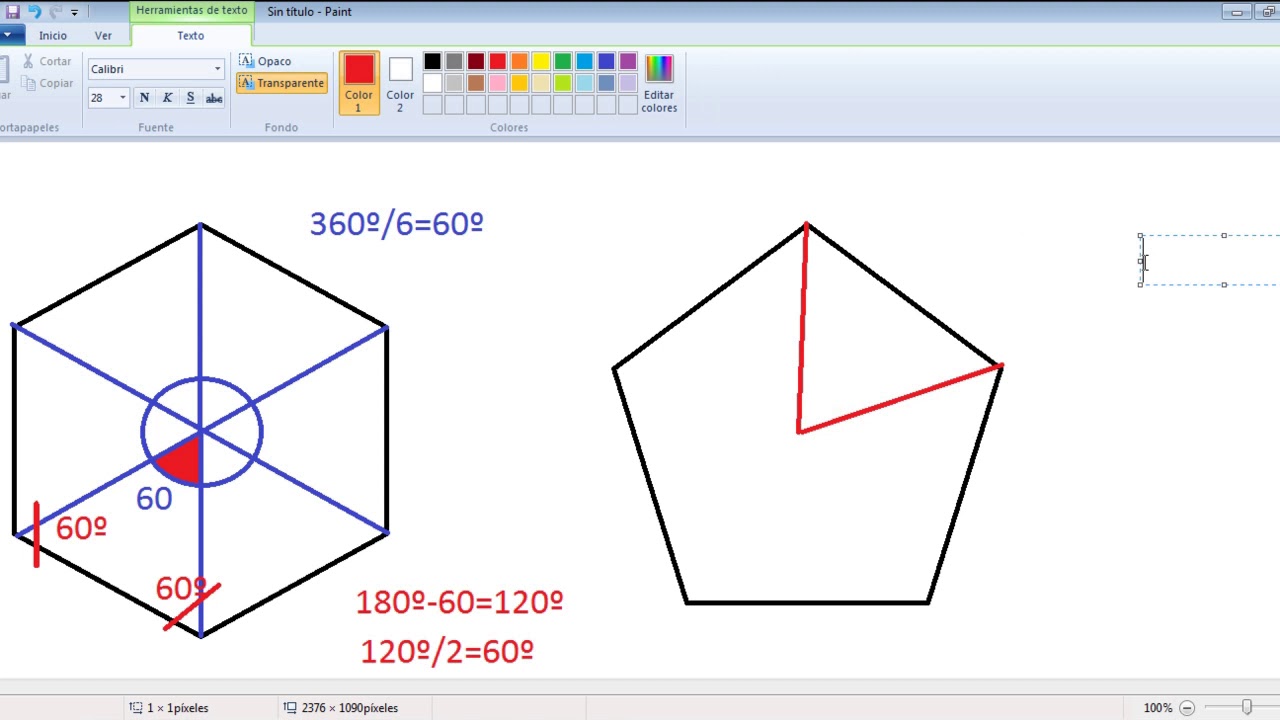
¿Por qué es importante la división de polígonos en triángulos?
La división de polígonos en triángulos es una técnica fundamental en matemáticas y geometría. Estos triángulos pueden facilitar cálculos y análisis más complejos al descomponer una figura en partes más sencillas.
¿Cómo dividir un polígono en triángulos?
Hay varias formas de dividir un polígono en triángulos, dependiendo de la figura y de lo que se quiera lograr. A continuación, veremos algunas técnicas comunes:
Trazar diagonales
Una forma sencilla de dividir un polígono en triángulos es trazar diagonales desde un vértice a los otros vértices. Esto crea triángulos más pequeños dentro del polígono original.
Ejemplo:
Consideremos un cuadrado. Si trazamos una diagonal desde un vértice opuesto, obtendremos dos triángulos congruentes en el interior del cuadrado.
Trazar alturas
Otra forma de dividir un polígono en triángulos es trazar alturas desde los vértices del polígono hasta los lados opuestos. Esto crea triángulos rectángulos dentro del polígono original.
Ejemplo:
Tomemos un triángulo equilátero. Si trazamos alturas desde cada vértice hasta el lado opuesto, obtendremos tres triángulos rectángulos congruentes dentro del triángulo equilátero.
Utilizar técnicas de división más complejas
En algunos casos, puede ser necesario utilizar técnicas de división más complejas, como el método de corte y costura o la partición en triángulos más pequeños. Estas técnicas son especialmente útiles cuando se trabaja con polígonos irregulares.
Ejemplo:
Imaginemos un polígono convexo con varios lados. Para dividirlo en triángulos, podemos utilizar el método de corte y costura, trazando líneas rectas desde un vértice a otro, creando triángulos más pequeños que se ajusten al polígono original.
Aplicaciones de la división de polígonos en triángulos
La división de polígonos en triángulos tiene muchas aplicaciones prácticas en varios campos, como la arquitectura, la cartografía, la ingeniería y la computación gráfica. Algunas de estas aplicaciones incluyen:
Calculando áreas y perímetros
Al dividir un polígono en triángulos, podemos calcular fácilmente el área y el perímetro total sumando las áreas y longitudes de los triángulos individuales.
Análisis de estructuras
La división de polígonos en triángulos es útil para el análisis de estructuras tridimensionales, como puentes y edificios. Al descomponer el polígono en triángulos, podemos determinar la estabilidad y la resistencia de la estructura.
Visualización de datos y gráficos
En la computación gráfica y la visualización de datos, la división de polígonos en triángulos es esencial para crear modelos 3D realistas y representar gráficamente información compleja.
Conclusiones
La división de polígonos en triángulos es una técnica fundamental en matemáticas y geometría. Permite realizar cálculos más sencillos y análisis más precisos al descomponer figuras complejas en partes más simples. Además, tiene numerosas aplicaciones en campos como la arquitectura, la ingeniería y la cartografía. Al utilizar estas técnicas, podemos comprender mejor las propiedades y características de los polígonos, así como analizar y visualizar datos de manera efectiva.
Preguntas frecuentes
1. ¿Es posible dividir cualquier polígono en triángulos?
Sí, es posible dividir cualquier polígono en triángulos utilizando diversas técnicas de división. Sin embargo, el número y la forma de los triángulos pueden variar dependiendo de la geometría del polígono original.
2. ¿Cuál es la ventaja de dividir un polígono en triángulos?
La división de polígonos en triángulos facilita el cálculo de áreas, perímetros y otras propiedades geométricas. Además, al descomponer una figura en triángulos, podemos comprender mejor su estructura y realizar análisis más precisos.
3. ¿Cuál es la aplicación más común de la división de polígonos en triángulos?
Una de las aplicaciones más comunes de la división de polígonos en triángulos es en la computación gráfica. Al utilizar triángulos, es posible representar modelos 3D y visualizar datos complejos de manera efectiva.