¿Por qué dividir un segmento en dos partes iguales?
Dividir un segmento en dos partes iguales es una técnica común en matemáticas y geometría. Esta división equitativa es útil para diversos propósitos, como encontrar puntos medios, construir triángulos o resolver problemas relacionados con áreas y volúmenes. En este artículo, exploraremos diferentes métodos para dividir segmentos en dos partes iguales y cómo aplicar estos conceptos en situaciones prácticas.
Cómo encontrar el punto medio de un segmento
El punto medio de un segmento es el punto que divide el segmento en dos partes iguales. Para encontrar el punto medio, seguimos estos pasos:
Paso 1: Dibuja el segmento
Comencemos trazando un segmento en una hoja de papel o en un programa de dibujo. Asegúrate de que el segmento sea lo suficientemente largo para trabajar con él visualmente.
Paso 2: Etiqueta los extremos del segmento
Asigna nombres o letras a los extremos del segmento. Esto nos ayudará a visualizar mejor el proceso de división.
Paso 3: Traza una línea recta que una los extremos
Usando una regla o una escuadra, traza una línea recta que una los dos extremos del segmento. Esta línea debe cruzar el segmento y extenderse más allá de él.
Paso 4: Encuentra el punto de intersección
Donde la línea recta que trazamos en el paso anterior intersecta al segmento, encontramos el punto medio. Marca este punto con una pequeña cruz o con una letra específica.
Paso 5: Verificación
Para confirmar que hemos encontrado el punto medio correctamente, podemos medir la distancia entre los extremos del segmento y el punto medio. Si esta distancia es igual en ambos lados, hemos dividido el segmento en dos partes iguales.
Aplicaciones prácticas de la división de segmentos
La técnica de dividir un segmento en dos partes iguales tiene numerosas aplicaciones prácticas en campos como la arquitectura, la ingeniería y la geometría. Algunas de estas aplicaciones incluyen:
Construcción de triángulos equiláteros
Al dividir un lado de un triángulo en dos partes iguales, podemos construir triángulos equiláteros, en los que todos los lados son iguales. Esto es útil para realizar diseños simétricos o al calcular áreas y perímetros.
División de una línea en segmentos proporcionales
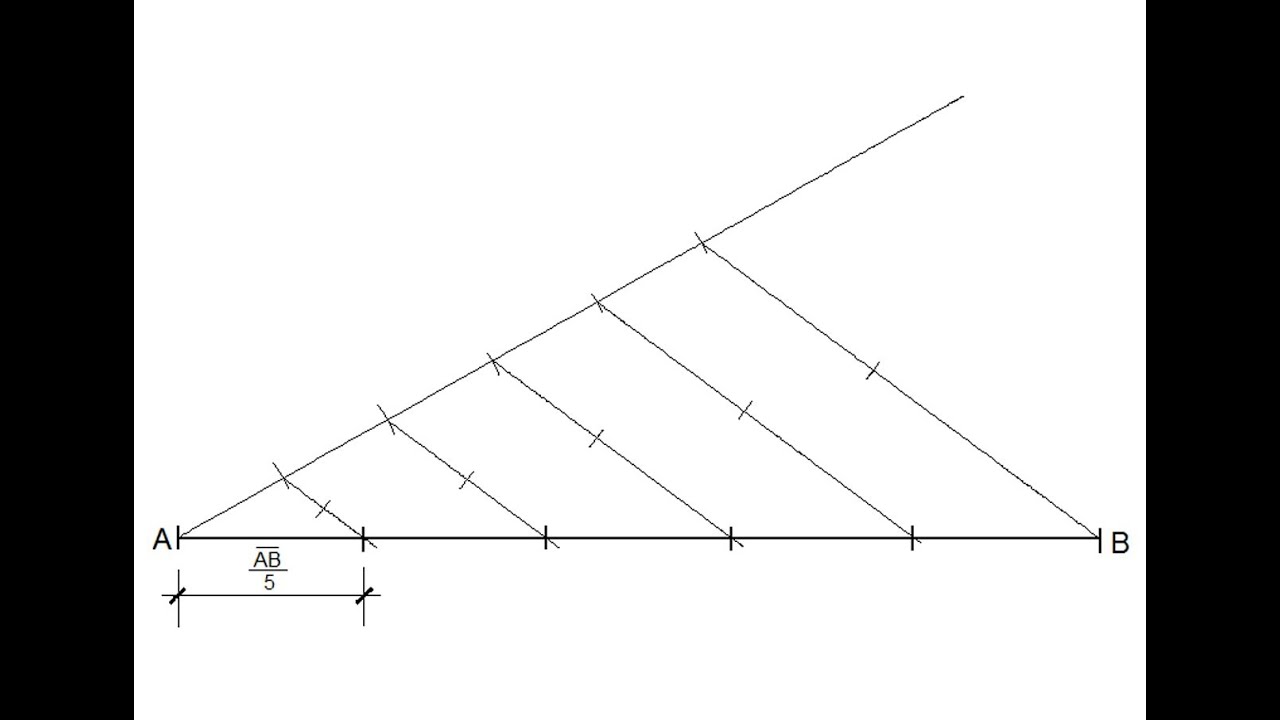
Dividir un segmento en partes proporcionales implica dividirlo en partes que están en una relación de proporción específica. Esto se utiliza en diversas aplicaciones, como la división de tierras agrícolas en parcelas de diferentes tamaños o la asignación de recursos en una empresa.
Construcción de polígonos regulares
Un polígono regular tiene todos sus lados y ángulos iguales. Al dividir un lado de un polígono regular en dos partes iguales, podemos construir polígonos regulares de diferentes tamaños. Esta técnica es útil al realizar diseños gráficos o al modelar estructuras en 3D.
Preguntas frecuentes sobre la división de segmentos
¿Es posible dividir un segmento en tres partes iguales?
Sí, es posible dividir un segmento en tres partes iguales utilizando técnicas adicionales, como la construcción del triángulo equilátero inscrito. Sin embargo, esto requiere pasos más complejos y no será abordado en este artículo.
¿Cómo se relaciona la división de segmentos con la geometría analítica?
La división de segmentos se puede abordar tanto en la geometría plana como en la geometría analítica. En la geometría analítica, podemos utilizar coordenadas cartesianas para determinar las coordenadas del punto medio de un segmento o para calcular la distancia entre los puntos.
¿Es posible dividir un segmento en partes desiguales?
Sí, es posible dividir un segmento en partes desiguales utilizando técnicas de proporción o utilizando herramientas matemáticas más avanzadas, como la regla y el compás. En este artículo, nos enfocamos en la división equitativa del segmento en dos partes iguales para simplificar el proceso y brindar una base sólida para futuras exploraciones.
¿Cuál es la importancia de la división equitativa de segmentos?
La división equitativa de segmentos es fundamental en muchos campos y disciplinas. Proporciona una base sólida para futuros cálculos y construcciones y nos permite trabajar con medidas precisas y proporcionales. Además, nos ayuda a comprender mejor los conceptos de simetría y proporción en la geometría y a aplicarlos en situaciones prácticas y reales.
Espero que este artículo haya sido útil para comprender la importancia y el proceso de dividir un segmento en dos partes iguales. La división de segmentos es una herramienta fundamental en matemáticas y geometría, y su aplicación se extiende a muchas otras áreas de estudio. Experimenta con los conceptos y aplica estos métodos en tus propias exploraciones y proyectos. ¡Diviértete descubriendo todo lo que puedes lograr con la división de segmentos!