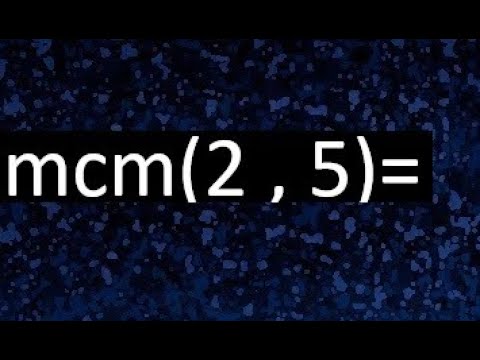Definición del Mínimo Común Múltiplo (MCM)
El Mínimo Común Múltiplo (MCM) es un concepto matemático que se utiliza para encontrar el número más pequeño que es divisible por dos o más números enteros.
En otras palabras, el MCM es el número común más pequeño que se puede encontrar multiplicando el número original por algún factor, de modo que el resultado sea un número entero.
Para encontrar el MCM de dos o más números, se pueden utilizar diferentes métodos, como el método de descomposición en factores primos y el método de la lista de múltiplos.
El método de descomposición en factores primos consiste en descomponer cada número en factores primos y luego tomar los factores comunes y no comunes elevados al mayor exponente. El resultado será el MCM.
Por ejemplo, si queremos encontrar el MCM de 6 y 8, descompondríamos los números en factores primos: 6 = 2^1 * 3^1 y 8 = 2^3. Luego, tomamos los factores comunes y no comunes elevados al mayor exponente: 2^3 * 3^1 = 24. Por lo tanto, el MCM de 6 y 8 es 24.
El método de la lista de múltiplos consiste en hacer una lista de los múltiplos de cada número y encontrar el primer múltiplo común. El resultado será el MCM.
Por ejemplo, si queremos encontrar el MCM de 4, 6 y 9, hacemos una lista de los múltiplos de cada número: 4 (4, 8, 12, 16, 20, 24, 28, 32, 36, 40…), 6 (6, 12, 18, 24, 30, 36, 42, 48, 54, 60…) y 9 (9, 18, 27, 36, 45, 54, 63, 72, 81, 90…). El primer múltiplo común que encontramos es 36. Por lo tanto, el MCM de 4, 6 y 9 es 36.
En conclusión
El Mínimo Común Múltiplo (MCM) es el número más pequeño que es divisible por dos o más números enteros. Se puede encontrar utilizando diferentes métodos, como el método de descomposición en factores primos y el método de la lista de múltiplos.
MCM de 2 y 5
Para encontrar el MCM (Mínimo Común Múltiplo) de 2 y 5, necesitamos listar los múltiplos de cada número y encontrar el menor número en común.
Múltiplos de 2:
- 2
- 4
- 6
- 8
- 10
- 12
- 14
- 16
- 18
- 20
Múltiplos de 5:
- 2
- 5
- 10
- 15
- 20
- 25
- 30
- 35
- 40
- 45
Como puedes ver, el primer número en común en las listas de múltiplos es 10. Por lo tanto, el MCM de 2 y 5 es 10.
En resumen, el MCM de 2 y 5 es 10.
Cálculo del MCM de 2 y 5
En matemáticas, el MCM o Mínimo Común Múltiplo es el valor más pequeño que es divisible por dos o más números.
Para calcular el MCM de 2 y 5, primero debemos encontrar los múltiplos de cada número y buscar el menor que sea común a ambos.
Múltiplos de 2: 2, 4, 6, 8, 10, 12, …
Múltiplos de 5: 5, 10, 15, 20, 25, 30, …
Observamos que el primer múltiplo común a ambos números es 10. Por lo tanto, el MCM de 2 y 5 es 10.
En resumen, el cálculo del MCM de 2 y 5 consiste en encontrar el menor múltiplo común a ambos números, que en este caso es 10.
Aplicaciones del MCM
El MCM, o Mínimo Común Múltiplo, es un concepto matemático ampliamente utilizado en diversas aplicaciones. A continuación, te presento algunas de las principales aplicaciones del MCM:
1. Matemáticas
El MCM se utiliza frecuentemente en problemas de matemáticas, especialmente en fracciones y proporciones. Permite encontrar el denominador común más pequeño para poder sumar, restar o comparar fracciones de manera más sencilla. Además, también es útil en problemas de multiplicación y división.
2. Tiempo y calendarios
El MCM es utilizado para determinar los intervalos de tiempo o calendarios que se repiten regularmente. Por ejemplo, si se desea saber cada cuántos años volverán a coincidir dos fechas especiales, se puede utilizar el MCM de los períodos de tiempo en que ocurren dichas fechas.
3. Programación y algoritmos
En programación, el MCM puede ser útil para determinar cuántas veces se repetirá un ciclo o bucle antes de que se cumpla una condición. También se utiliza para sincronizar procesos o tareas que deben ejecutarse de manera simultánea o en intervalos regulares.
4. Sistemas eléctricos
En sistemas eléctricos, el MCM ayuda a determinar el tiempo en que se repiten las señales o ciclos eléctricos, lo que resulta fundamental en diversas aplicaciones, como la transmisión de datos, la generación de señales periódicas y la regulación de corriente en circuitos.
5. Logística y distribución
En el ámbito de la logística y distribución, el MCM se utiliza para determinar el mínimo tiempo en que se debe reabastecer un producto o servicio en diferentes puntos de venta o distribución. Esto permite una gestión eficiente de inventario y una planificación adecuada de envíos.
En conclusión, el MCM tiene una amplia variedad de aplicaciones en distintos campos, desde las matemáticas y la programación hasta la logística y la distribución. Su capacidad para encontrar el denominador común más pequeño o determinar intervalos de tiempo repetitivos lo convierte en una herramienta indispensable en muchas situaciones.