Mínimo común múltiplo de 28 35 y 63

¿Qué es el mínimo común múltiplo (MCM)?

El mínimo común múltiplo (MCM) es el menor múltiplo común de dos o más números. Es decir, es el número más pequeño que puede ser dividido de manera exacta por todos los números dados.

Para calcular el MCM, se deben encontrar todos los múltiplos de los números dados hasta que se encuentre el primer múltiplo común. El número encontrado será el MCM.

Por ejemplo, los múltiplos de 4 son: 4, 8, 12, 16, 20, …, y los múltiplos de 6 son: 6, 12, 18, 24, 30, … El primer múltiplo común de 4 y 6 es 12, por lo tanto, el MCM de 4 y 6 es 12.

El MCM es utilizado en diversas áreas de las matemáticas, como en la resolución de problemas de fracciones, ecuaciones algebraicas y la simplificación de expresiones algebraicas.

Propiedades del mínimo común múltiplo:

1. Multiplicación por un número: El MCM de un número multiplicado por otro número es igual al producto de los MCM de cada número por separado.
2. Múltiplo común: Si un número es múltiplo de todos los números dados, entonces también es múltiplo del MCM de los números dados.
3. Mínimo: El MCM es el menor múltiplo común posible. No hay otro número menor que pueda ser dividido de manera exacta por todos los números dados.

En conclusión, el MCM es un concepto fundamental en matemáticas que nos permite encontrar el menor múltiplo común de dos o más números. Su cálculo se basa en encontrar los múltiplos comunes de los números dados y seleccionar el menor de ellos. El MCM se utiliza en diversas ramas de las matemáticas y es de gran utilidad para realizar operaciones con fracciones, ecuaciones y expresiones algebraicas.

Método 1: Descomposición de factores primos

La descomposición de factores primos es un método utilizado en matemáticas para descomponer un número en sus factores primos. Este método nos permite expresar un número como la multiplicación de números primos.

¿Qué son los factores primos?
Los factores primos son los números primos que dividen exactamente a un número dado, es decir, no dejan residuo. Por ejemplo, los factores primos de 24 son 2, 2, 2 y 3, ya que 2 x 2 x 2 x 3 = 24.

Pasos para la descomposición de factores primos:
1. Comenzamos dividiendo el número dado por el número primo más pequeño posible. Si el número es divisible por ese número, lo anotamos como un factor y dividimos el número original por ese factor.
2. Continuamos dividiendo el número resultante por el siguiente número primo y repitiendo el proceso hasta que obtengamos un cociente de 1.

Ejemplo:
Tomemos el número 56 como ejemplo para ilustrar la descomposición de factores primos.
1. Empezamos dividiendo 56 por 2. Como 56 es divisible por 2, anotamos 2 como un factor y obtenemos un cociente de 28.
2. Continuamos dividiendo 28 por 2. Nuevamente, es divisible por 2, por lo que anotamos otro 2 como un factor y obtenemos un cociente de 14.
3. Dividimos 14 por 2 una vez más, pero esta vez no es divisible. Procedemos a dividirlo por el siguiente número primo, que es 3. Obtenemos un cociente de 7.
4. Por último, dividimos 7 por sí mismo, ya que es un número primo. Obtenemos un cociente de 1.

Por lo tanto, la descomposición de factores primos de 56 es 2 x 2 x 2 x 7.

En resumen, el método de descomposición de factores primos es una forma eficiente de encontrar los factores primos de un número y expresarlo como multiplicación de dichos factores. Este método es ampliamente utilizado en matemáticas y tiene aplicaciones en diversas áreas.

Método 2: Método del producto

Uno de los métodos más utilizados para resaltar las frases más importantes en un texto HTML es el Método del Producto. Este método consiste en utilizar etiquetas HTML como o para hacer que ciertas frases sobresalgan y capturen la atención del lector.

Además de estas etiquetas, también se pueden utilizar otros elementos HTML para resaltar aún más las frases importantes, como los encabezados

o las listas en HTML.

Al utilizar las etiquetas o , se logra poner en negritas las frases que deseamos resaltar, lo cual las hace llamar la atención y destacar visualmente. Esto puede ser especialmente útil en textos largos o en párrafos donde se desea enfatizar cierta información clave.

Por otro lado, los encabezados

también permiten resaltar frases importantes al darles un formato de título. Esto no solo las hace más visibles, sino que también indica la importancia de dichas frases dentro del texto.

Finalmente, las listas en HTML son otro recurso muy útil para resaltar información relevante. Ya sea una lista numerada o una lista con viñetas, el uso de este elemento permite presentar de manera clara y ordenada las frases importantes del texto.

En resumen, el Método del Producto es una técnica efectiva para resaltar frases importantes en un texto HTML. Al utilizar etiquetas como , ,

y listas en HTML, se logra llamar la atención del lector y destacar la información clave del texto.

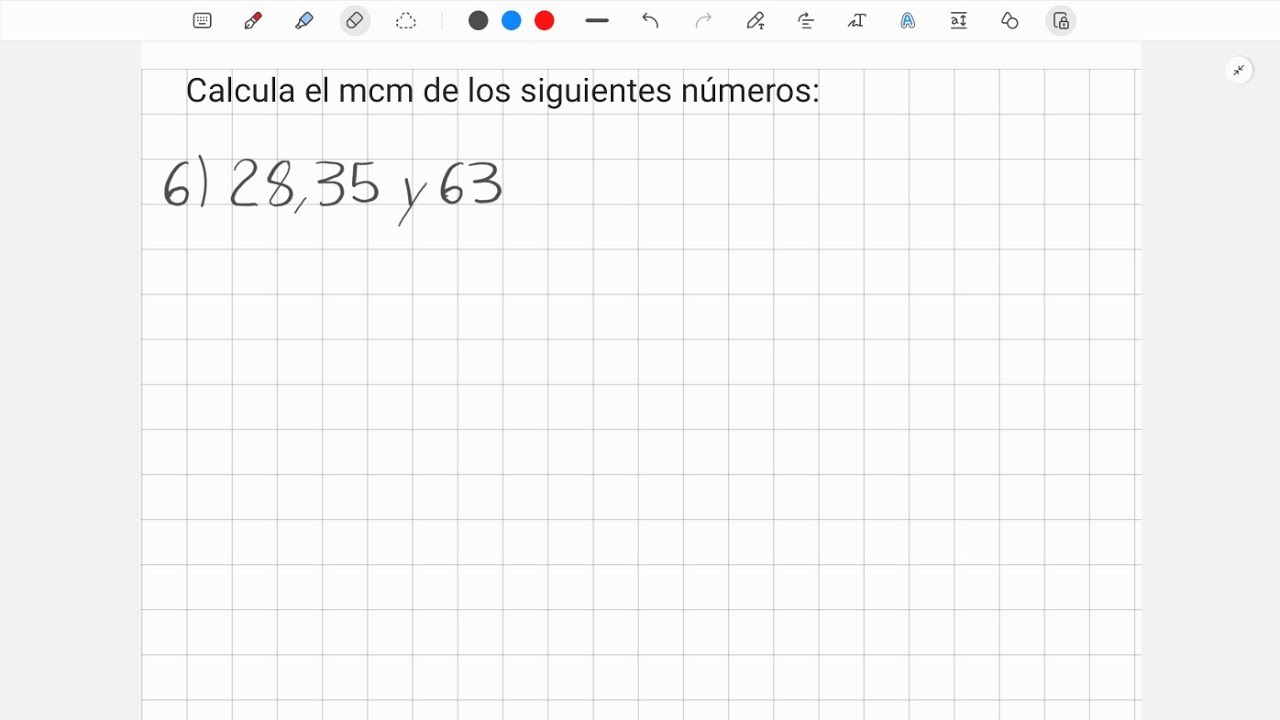
Resultado: MCM de 28, 35 y 63

1. Encontrar el MCM (Mínimo Común Múltiplo) de tres números puede ser un proceso interesante pero muy útil.
2. En este caso, tenemos los números 28, 35 y 63 de los cuales queremos encontrar su MCM.
3. El MCM es el número más pequeño que es múltiplo de todos los números dados.
4. Para encontrar el MCM, es necesario desglosar cada número en sus factores primos.
5. Para el 28, sus factores primos son 2x2x7.
6. Para el 35, sus factores primos son 5×7.
7. Y para el 63, sus factores primos son 3x3x7.
8. Ahora, debemos tomar cada factor primo que aparece en los números y multiplicar la mayor cantidad de veces que aparece.
9. En este caso, el factor primo 2 aparece dos veces, el factor primo 3 aparece dos veces y el factor primo 5 aparece una vez.
10. Entonces, multiplicamos 2x2x3x3x5 y obtenemos 180.
11. Por lo tanto, el MCM de 28, 35 y 63 es 180.

Aplicaciones del MCM

El mínimo común múltiplo (MCM) es un concepto matemático que tiene diversas aplicaciones en diferentes áreas. Algunas de estas aplicaciones son:

1. Matemáticas:

• Descomposición: El MCM se utiliza para descomponer fracciones en partes más simples, lo que facilita realizar operaciones matemáticas con ellas.
• Operaciones con fracciones: El MCM se utiliza para realizar sumas, restas, multiplicaciones y divisiones con fracciones que tienen denominadores diferentes.
• Cálculo de probabilidad: El MCM se utiliza para calcular la probabilidad de que ocurra un evento periódico en un cierto período de tiempo.

2. Organización de eventos:

• Planificación de horarios: El MCM se utiliza para organizar el horario de eventos periódicos, como reuniones, conferencias, clases, entre otros.
• Programación de actividades: El MCM se utiliza para distribuir y programar actividades en eventos múltiples que ocurren simultáneamente.

3. Informática:

• Optimización de algoritmos: El MCM se utiliza para optimizar el rendimiento de algoritmos que tienen ciclos y repeticiones.
• Organización de datos: El MCM se utiliza para organizar y sincronizar el acceso a datos en sistemas distribuidos.

En resumen, el MCM tiene aplicaciones importantes en matemáticas, organización de eventos e informática. Su comprensión y uso adecuado nos permite resolver problemas de manera más eficiente y efectiva en diversas áreas de estudio y trabajo.