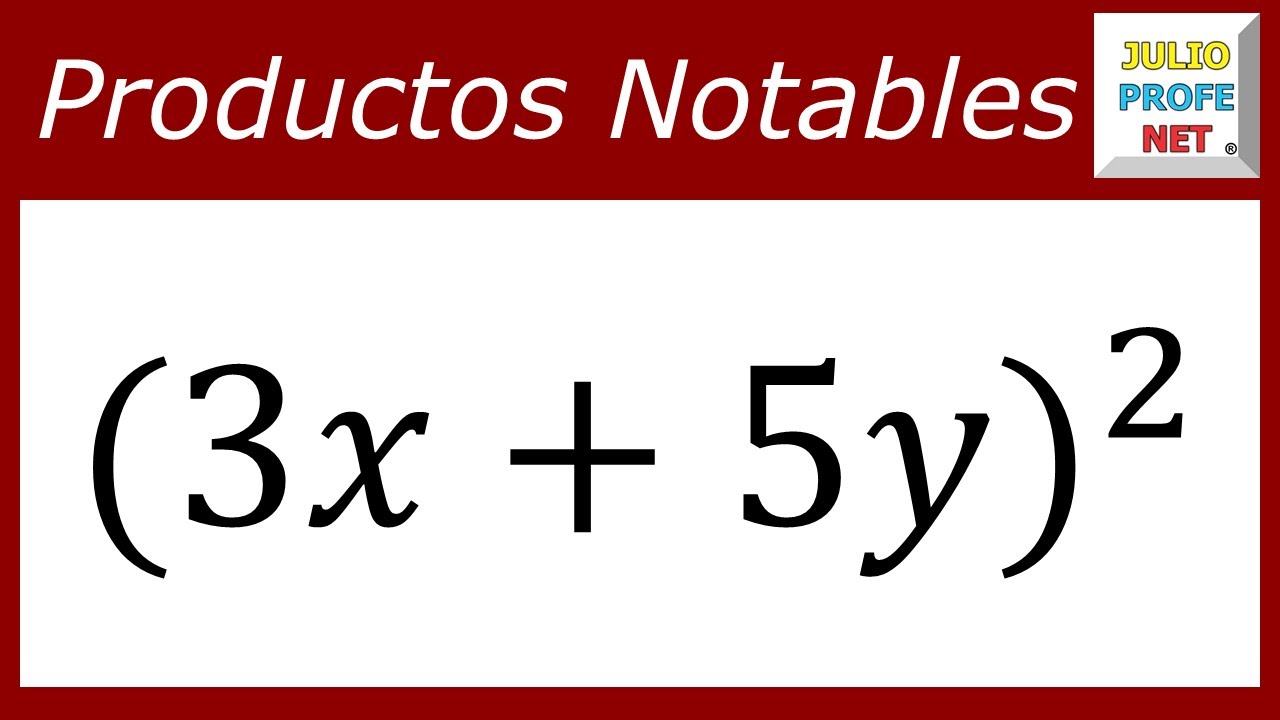¿Qué es un binomio?
Un binomio es un término algebraico que consta de dos términos separados por una operación de suma o resta. Los términos individuales dentro del binomio pueden ser números o variables. Los binomios son una parte fundamental de la álgebra y se utilizan en una variedad de situaciones, incluyendo la factorización, la simplificación de expresiones y la resolución de ecuaciones.
Cuando hablamos de un binomio, generalmente se nos refiere a un binomio cuadrado perfecto, que es una forma especial de binomio. Un binomio cuadrado perfecto es el resultado de multiplicar un binomio consigo mismo. Por ejemplo, (a+b)^2 es un binomio cuadrado perfecto.
Los binomios pueden ser clasificados en diferentes categorías:
1. Binomio monomio: Un binomio monomio es un binomio compuesto por un término constante y un término lineal. Ejemplo: 5x + 2.
2. Binomio cuadrado perfecto: Un binomio cuadrado perfecto es aquel cuyo resultado de multiplicar el binomio consigo mismo produce un trinomio cuadrado perfecto. Ejemplo: (x+2)^2 = x^2 + 4x + 4.
3. Binomio conjugado: Un binomio conjugado es un binomio en el que los términos son idénticos, excepto uno tiene signo positivo y el otro tiene signo negativo. Ejemplo: (a+b) y (a-b) son binomios conjugados.
4. Binomio opuesto: Un binomio opuesto es un binomio en el que los términos son iguales, excepto uno tiene signo positivo y el otro tiene signo negativo. Ejemplo: (a+b) y (-a-b) son binomios opuestos.
En conclusión, un binomio es un término algebraico compuesto por dos términos separados por una operación de suma o resta. Los binomios se utilizan en varias áreas de las matemáticas y son clasificados en diferentes categorías como binomios monomios, binomios cuadrados perfectos, binomios conjugados y binomios opuestos.
Fórmula para obtener el cuadrado de un binomio
La fórmula para obtener el cuadrado de un binomio se conoce como identidad del cuadrado de la suma y se representa de la siguiente manera:
(a + b)2 = a2 + 2ab + b2
Donde a y b son los términos del binomio.
Esta fórmula se utiliza para expandir y simplificar expresiones algebraicas que estén en forma de un binomio al cuadrado. Al aplicar la fórmula, debemos elevar al cuadrado cada término del binomio y luego distribuir el resultado de la multiplicación.
Podemos visualizar la fórmula de manera más clara si representamos los términos dentro de una lista:
- a2 – representa el cuadrado del primer término a.
- 2ab – representa el producto de los términos a y b multiplicados por 2.
- b2 – representa el cuadrado del segundo término b.
Es importante recordar que la fórmula del cuadrado de un binomio solo es aplicable cuando se trata de un binomio al cuadrado. Para obtener el cuadrado de otra expresión algebraica más compleja, es necesario utilizar fórmulas o propiedades más específicas.
¡Ahora que conoces la fórmula para obtener el cuadrado de un binomio, podrás simplificar de manera más eficiente expresiones algebraicas que se presenten en esta forma!
Ejemplo
En este ejemplo, vamos a utilizar etiquetas HTML para resaltar las frases más importantes del texto. Usaremos la etiqueta <strong> para enfatizar estas frases.
Frases importantes:
- En este ejemplo, vamos a utilizar etiquetas HTML para resaltar las frases más importantes del texto.
- Usaremos la etiqueta <strong> para enfatizar estas frases.
También podemos utilizar la etiqueta <b> para poner el texto en negrita:
Otras frases importantes:
- Utilizaremos etiquetas HTML para mejorar el diseño y la estructura de nuestras páginas web.
- Las etiquetas HTML nos permiten dar estilo y formato a nuestro contenido.
En resumen, las etiquetas HTML nos brindan la posibilidad de resaltar y dar énfasis a ciertas frases importantes en nuestros textos, mejorando así la legibilidad y la estructura de nuestras páginas web.
Aplicaciones del cuadrado de un binomio
El cuadrado de un binomio es una expresión algebraica que se obtiene al multiplicar un binomio por sí mismo. Tiene diversas aplicaciones en matemáticas y otras áreas, que vamos a explorar a continuación:
1. Expansión de binomios
Una de las aplicaciones más comunes del cuadrado de un binomio es la expansión de binomios. Al multiplicar un binomio por sí mismo, se obtiene una expresión algebraica que puede simplificarse y descomponerse en términos individuales. Esto es especialmente útil en la resolución de ecuaciones o identidades matemáticas.
2. Geometría
En geometría, el cuadrado de un binomio tiene aplicaciones en el cálculo del área de figuras geométricas. Por ejemplo, si se tiene un cuadrado con lado “a” y se desea calcular el área de un cuadrado que tiene el doble de lado, se puede expresar el área como el cuadrado de la suma de “a” y “a”. Esto se representa como (a + a)^2.
3. Probabilidad
En probabilidad y estadística, el cuadrado de un binomio puede utilizarse para calcular la probabilidad de eventos específicos. Por ejemplo, al lanzar dos dados, se puede utilizar el cuadrado de la suma de los resultados posibles para calcular la probabilidad de obtener una suma específica.
4. Física
En física, el cuadrado de un binomio puede tener aplicaciones en el cálculo de fuerzas o en la resolución de problemas relacionados con el movimiento. Por ejemplo, al calcular la velocidad final de un objeto en caída libre, se puede utilizar el cuadrado de la suma de la velocidad inicial y el doble del producto de la aceleración y el tiempo.
5. Estadística
En estadística, el cuadrado de un binomio puede utilizarse en la resolución de problemas de probabilidad condicional o en el cálculo de la varianza de una muestra. Además, también puede ser utilizado en la elaboración de modelos matemáticos para predecir resultados o evaluar comportamientos.
En resumen, el cuadrado de un binomio tiene múltiples aplicaciones en matemáticas, geometría, probabilidad, física y estadística. Su uso no se limita solo a estas áreas, ya que puede tener aplicaciones en otros campos como la economía o las ciencias de la computación.
Conclusión
En resumen, las etiquetas HTML son una parte fundamental a la hora de escribir contenido web, ya que nos permiten estructurar y dar formato a nuestras páginas de manera efectiva.
Al utilizar la etiqueta <strong>, podemos destacar las frases más importantes del texto, resaltando así su relevancia para el lector.
Beneficios de utilizar etiquetas HTML
- Mejor organización del contenido.
- Mayor legibilidad y claridad.
- Facilita la navegación del usuario.
- Mejora el posicionamiento en los motores de búsqueda.
También podemos utilizar la etiqueta <b>, que nos permite resaltar texto mediante el uso de negritas.
Es importante tener en cuenta que aunque estas etiquetas pueden mejorar la presentación de nuestro contenido, no debemos abusar de ellas, ya que un uso excesivo puede dificultar la lectura y comprensión.
En conclusión, utilizar las etiquetas HTML adecuadas nos ayudará a crear páginas web más claras, organizadas y atractivas visualmente, lo cual es fundamental para brindar una buena experiencia de usuario.