1. Ángulo central
En geometría, el ángulo central se refiere a un tipo de ángulo que se forma en el centro de una circunferencia. Se denomina así porque su vértice está en el centro de la figura.
El ángulo central es importante en diversos contextos, como en la trigonometría y en la geometría analítica. En trigonometría, el ángulo central se utiliza para medir los ángulos en relación con la unidad de medida de la circunferencia, el ángulo radian. En geometría analítica, el ángulo central es utilizado para definir la posición de un punto en un plano cartesiano.
El ángulo central puede ser medido en grados o en radianes. En grados, la circunferencia completa se divide en 360 partes iguales, por lo que el ángulo central se mide de 0 a 360 grados. En radianes, la circunferencia completa se divide en 2π partes iguales, por lo que el ángulo central se mide de 0 a 2π radianes.
El ángulo central es especialmente importante en los estudios de geometría euclidiana. Se utiliza para describir las propiedades de los círculos y sus relaciones con otros elementos geométricos, como los arcos y las cuerdas.
En resumen, el ángulo central es un importante concepto en geometría que se utiliza para medir los ángulos en relación con el centro de una circunferencia. Su estudio es fundamental para comprender las propiedades de los círculos y su relación con otras figuras geométricas.
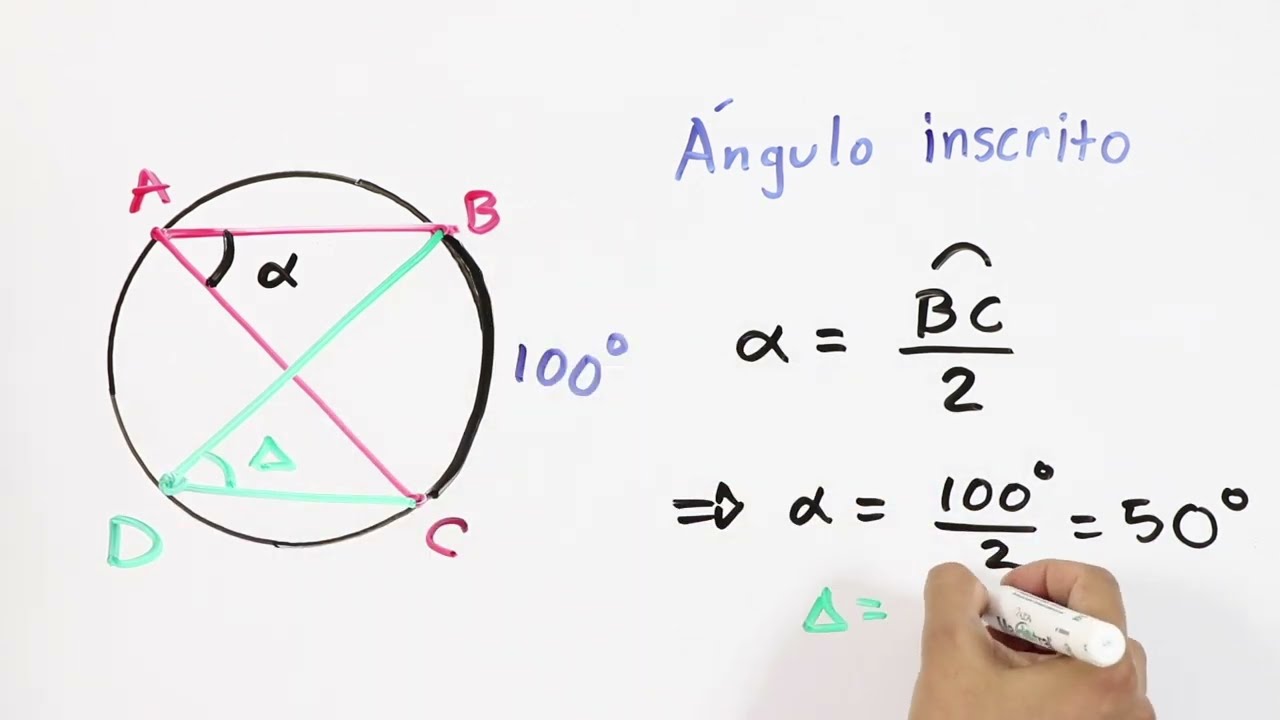
2. Ángulo inscrito
El ángulo inscrito es aquel que se encuentra dentro de una circunferencia y tiene sus extremos sobre la misma circunferencia.
Para entender mejor este concepto, es importante recordar que una circunferencia está compuesta por un conjunto de puntos equidistantes a un centro. Los ángulos inscritos se forman cuando trazamos dos líneas desde el centro de la circunferencia hasta dos puntos en la circunferencia misma.
Uno de los aspectos más interesantes de los ángulos inscritos es que tienen la propiedad de ser la mitad de un ángulo central. Un ángulo central es aquel que se forma cuando trazamos dos líneas desde el centro de la circunferencia hasta los extremos de un arco.
Por ejemplo, si tenemos un arco que abarca 90 grados en una circunferencia, el ángulo central correspondiente será de 180 grados. En este caso, el ángulo inscrito será de 90 grados, ya que es la mitad del ángulo central.
Además, los ángulos inscritos que tienen los mismos extremos sobre la circunferencia son siempre iguales entre sí. Esto se debe a que la distancia entre el centro de la circunferencia y los puntos de intersección es siempre la misma.
Es importante tener en cuenta que los ángulos inscritos pueden tener diferentes medidas, incluso pueden ser de 0 grados o de 180 grados si los puntos de intersección están muy cerca o muy lejos del centro de la circunferencia.
En conclusión, el concepto de ángulo inscrito es fundamental para entender las relaciones geométricas dentro de una circunferencia. Su relación con los ángulos centrales y su propiedad de tener siempre la misma medida en casos específicos brindan herramientas útiles para resolver problemas de geometría.
3. Ángulo semiinscrito
Un ángulo semiinscrito es aquel que tiene su vértice en un punto de la circunferencia y sus lados son secantes a la misma. Este tipo de ángulo es muy relevante en geometría, ya que se utiliza en diversos problemas y demostraciones.
Para comprender mejor qué es un ángulo semiinscrito, es necesario entender algunos conceptos básicos de la geometría de la circunferencia. La circunferencia es una figura geométrica formada por todos los puntos que equidistan de un punto central llamado centro. Los puntos de la circunferencia se encuentran a una distancia constante del centro, conocida como radio.
Una circunferencia también tiene una medida llamada diámetro, que es la distancia entre dos puntos opuestos de la circunferencia y pasa necesariamente por el centro. A partir del diámetro, podemos definir un segmento de longitud igual a la mitad del diámetro, llamado radio.
Vamos a ver un caso práctico de un ángulo semiinscrito para entenderlo mejor. Supongamos que tenemos una circunferencia de radio 5 cm y un triángulo inscrito en ella. Este triángulo tiene un vértice en uno de los puntos de la circunferencia y sus lados son secantes a la misma.
En este caso, el ángulo semiinscrito sería el ángulo formado por uno de los lados del triángulo y la circunferencia. Si trazamos el radio que parte del centro de la circunferencia hasta uno de los extremos del lado del triángulo, el ángulo semiinscrito sería el ángulo formado entre este radio y el lado del triángulo.
Es importante destacar que la medida del ángulo semiinscrito depende del triángulo inscrito en la circunferencia, es decir, de la posición del vértice del triángulo en la circunferencia. Además, la medida de este ángulo también está relacionada con la medida del arco subtendido por dicho ángulo.
En resumen, un ángulo semiinscrito es aquel que tiene su vértice en un punto de la circunferencia y sus lados son secantes a la misma. Esta figura geométrica es relevante en problemas y demostraciones de geometría, y su medida depende del triángulo inscrito en la circunferencia y del arco subtendido por el ángulo.
4. Ángulo exterior
El ángulo exterior es un concepto fundamental en la geometría. Se define como el ángulo formado por un lado de un triángulo y la prolongación de su lado adyacente.
Para entender mejor este concepto, es necesario recordar que los ángulos en un triángulo suman 180 grados. Por lo tanto, si conocemos dos ángulos interiores de un triángulo, podemos calcular el tercer ángulo. Pero, ¿qué pasa si queremos calcular el ángulo que se forma fuera del triángulo? Aquí es donde entra en juego el ángulo exterior.
Para calcular el ángulo exterior de un triángulo, podemos utilizar la siguiente fórmula:
Ángulo Exterior = 180° – Ángulo Interior
Esta fórmula nos permite determinar el ángulo exterior con solo conocer uno de los ángulos interiores del triángulo. Es importante tener en cuenta que el ángulo exterior siempre será mayor que cualquiera de los ángulos interiores, ya que la suma de un ángulo interior y su ángulo exterior correspondiente siempre es igual a 180 grados.
En términos prácticos, el ángulo exterior nos permite identificar y medir las intersecciones entre diferentes líneas o segmentos en la geometría, lo que resulta útil en diversas aplicaciones, como la arquitectura, la ingeniería y la navegación.
En resumen, el ángulo exterior es aquel que se forma fuera de un triángulo y se calcula restando el ángulo interior correspondiente de 180 grados. Este concepto es fundamental para entender las relaciones angulares en la geometría y su aplicación en diversas áreas.
5. Ángulo secante
En trigonometría, el ángulo secante es una función que relaciona un ángulo con la longitud de la hipotenusa de un triángulo rectángulo. La función secante se denota como sec(x) y se calcula como el inverso de la función coseno.
La función secante es especialmente útil para calcular ángulos en trigonometría. Se utiliza para encontrar la medida de un ángulo en función de los lados del triángulo rectángulo. El ángulo secante es el inverso de la función coseno y se calcula dividiendo la hipotenusa entre el cateto adyacente.
Para calcular el ángulo secante, primero se debe determinar la hipotenusa y el cateto adyacente del triángulo rectángulo. Una vez que se tienen estos valores, se divide la hipotenusa entre el cateto adyacente y se obtiene el valor del ángulo secante.
Es importante tener en cuenta que la función secante solo se define en ciertos rangos de ángulos. En la mayoría de los casos, se utiliza en ángulos agudos o en el primer y segundo cuadrante del plano cartesiano.
Si se desea representar gráficamente el ángulo secante, se puede utilizar una función secante para trazar una curva que muestra cómo varía el valor del ángulo en función de los lados del triángulo rectángulo.
En conclusión, el ángulo secante es una función trigonométrica que relaciona un ángulo con la hipotenusa de un triángulo rectángulo. Esta función se utiliza para calcular ángulos y se representa gráficamente mediante una curva. Es importante tener en cuenta los rangos de ángulos en los que se define la función secante.