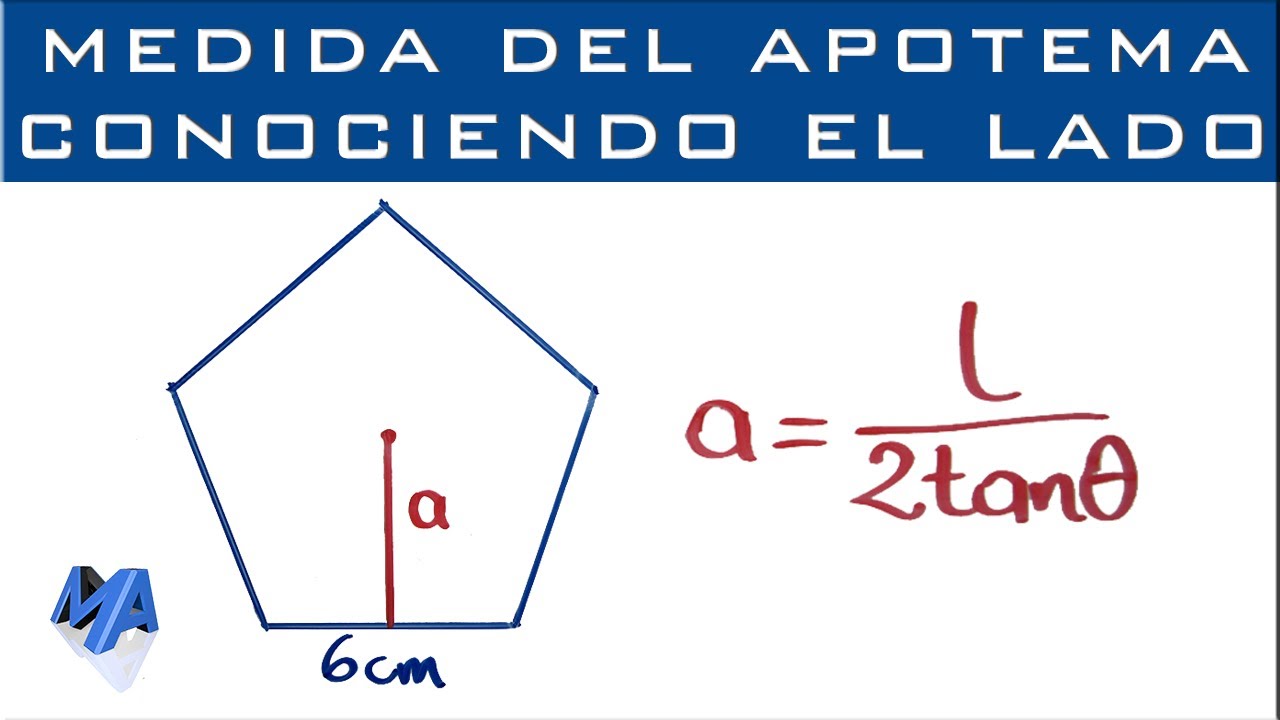
¿Qué es el apotema de un polígono regular?
El apotema es una medida geométrica muy importante en el estudio de los polígonos regulares. Pero, ¿qué es exactamente el apotema de un polígono regular? Para entenderlo de manera sencilla, podemos decir que el apotema es la distancia perpendicular desde el centro del polígono hasta cualquiera de sus lados. En otras palabras, es la distancia más corta entre el centro y uno de los lados del polígono. Esta medida también se conoce como la altura de cada triángulo isósceles formado por el centro, uno de los vértices y uno de los lados del polígono.
Importancia del apotema en los polígonos regulares
El apotema de un polígono regular tiene una gran importancia en diversas áreas de las matemáticas y la arquitectura. Por ejemplo, en geometría, el apotema nos permite calcular el área de un polígono regular mediante la fórmula A = (perímetro * apotema) / 2. Esta fórmula nos ayuda a encontrar el área sin necesidad de dividir el polígono en triángulos, lo que simplifica los cálculos.
En arquitectura y diseño, el apotema también es muy relevante. Permite calcular la altura de construcciones con formas poligonales, como torres o pilares, lo que facilita la planificación y el diseño de estructuras más estables y estéticamente agradables. También permite calcular la longitud de los lados de un polígono regular y determinar la posición del centro de gravedad de un objeto.
Apotema de un triángulo equilátero
Comencemos nuestro análisis del apotema con un polígono sencillo: el triángulo equilátero. Este tipo de triángulo tiene todos sus lados de la misma longitud y todos sus ángulos iguales, lo que lo convierte en uno de los más simples de estudiar.
¿Cómo se calcula el apotema de un triángulo equilátero?
Para calcular el apotema de un triángulo equilátero, podemos seguir un sencillo procedimiento. Primero, necesitaremos conocer la longitud de uno de los lados del triángulo. A partir de esta medida, podemos encontrar la altura del triángulo utilizando el teorema de Pitágoras.
Paso 1: Conocer la longitud de un lado del triángulo
Supongamos que la longitud de un lado del triángulo equilátero es a. En este caso, todos los lados tienen una longitud de a.
Paso 2: Calcular la altura utilizando el teorema de Pitágoras
El siguiente paso consiste en calcular la altura del triángulo, la cual corresponderá al apotema. Para hacerlo, podemos utilizar el teorema de Pitágoras, que establece que en un triángulo rectángulo, la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa.
Dado que el triángulo equilátero tiene todos sus ángulos iguales, podemos dividirlo en dos triángulos rectángulos iguales. La hipotenusa será uno de los lados del triángulo equilátero y los catetos serán la mitad de la longitud de un lado del triángulo y la altura que buscamos.
Aplicando el teorema de Pitágoras, obtendremos la fórmula para calcular la altura del triángulo:
h = √(a^2 – (a/2)^2)