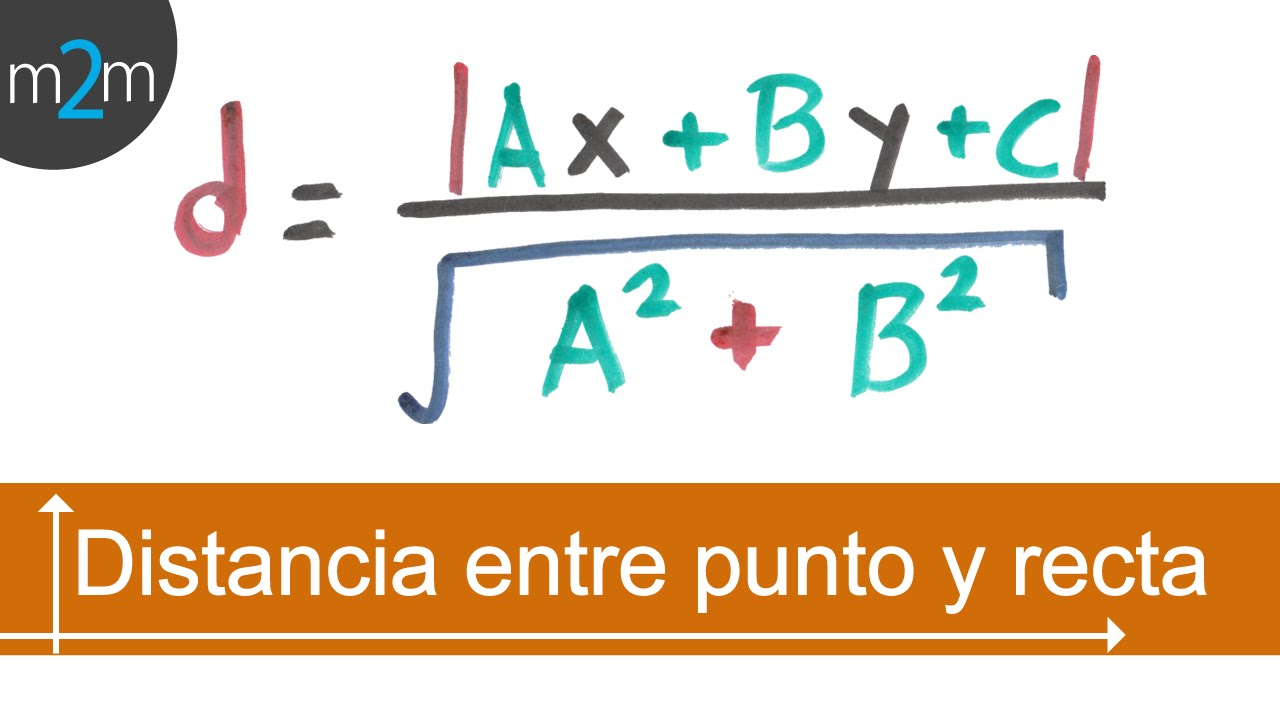
La distancia punto-recta es un concepto fundamental en geometría analítica que nos permite calcular la distancia entre un punto y una recta en el plano cartesiano. En este artículo, exploraremos este concepto en detalle y mostraremos cómo podemos aplicarlo en diversas situaciones.
¿Qué es la distancia punto-recta?
La distancia punto-recta se refiere a la longitud del segmento perpendicular trazado desde un punto dado a una recta en el plano cartesiano. Esta distancia es un valor numérico que nos indica cuánto debemos desplazarnos desde el punto hasta la recta siguiendo esta línea perpendicular.
¿Cómo se calcula la distancia punto-recta?
Para calcular la distancia entre un punto y una recta, necesitamos conocer las coordenadas del punto y una ecuación que represente a la recta. A continuación, presentamos un método paso a paso para realizar este cálculo:
Paso 1: Determinar la ecuación de la recta
El primer paso es obtener una ecuación que represente a la recta. Esto puede hacerse de varias formas, dependiendo del contexto y de la información disponible. Algunos métodos comunes incluyen:
- Usar la pendiente y un punto de la recta.
- Usar dos puntos de la recta.
- Usar la ecuación general de una recta.
Una vez que tenemos la ecuación de la recta, podemos proceder al siguiente paso.
Paso 2: Encontrar la ecuación de la recta perpendicular
Para calcular la distancia punto-recta, necesitamos trazar una línea perpendicular desde el punto hacia la recta. Para lograr esto, encontramos la pendiente negativa recíproca de la recta dada y la utilizamos para obtener la ecuación de la recta perpendicular.
Paso 3: Encontrar el punto de intersección
A continuación, encontramos el punto de intersección entre la recta perpendicular y la recta original. Esto se hace resolviendo el sistema de ecuaciones formado por ambas rectas.
Paso 4: Calcular la distancia
Finalmente, calculamos la distancia utilizando la fórmula de la distancia entre dos puntos. Tomamos el punto dado y el punto de intersección encontrado en el paso anterior, y calculamos la longitud del segmento que los une.
Aplicaciones de la distancia punto-recta
La distancia punto-recta tiene numerosas aplicaciones en diversos campos de estudio y en problemas prácticos. A continuación, presentamos algunas situaciones en las que podemos utilizar este concepto:
1. Geometría: Podemos utilizar la distancia punto-recta para determinar si un punto está dentro o fuera de una figura geométrica, como un polígono.
2. Física: En física, la distancia punto-recta se aplica en problemas relacionados con la trayectoria de objetos en movimiento, como calcular la distancia mínima entre un punto y una recta de acción.
3. Economía: En economía, la distancia punto-recta puede ayudarnos a encontrar la distancia mínima entre un punto de producción y una línea de distribución, optimizando así los costos de transporte.
4. Ingeniería: En ingeniería, la distancia punto-recta es útil para determinar la distancia mínima entre una estructura y una línea de alta tensión, garantizando la seguridad y evitando posibles accidentes.
5. Navegación: En navegación marítima o aérea, podemos utilizar la distancia punto-recta para calcular la distancia más corta entre un punto de partida y un destino, teniendo en cuenta las rutas de navegación disponibles.
Conclusión
La distancia punto-recta es un concepto fundamental que nos permite calcular la distancia entre un punto y una recta en el plano cartesiano. Este cálculo tiene numerosas aplicaciones en diversos campos de estudio y en problemas prácticos. Siempre que necesitemos determinar la distancia mínima entre un punto y una recta, podemos utilizar este concepto y seguir los pasos mencionados anteriormente.
Preguntas frecuentes
1. ¿Por qué es importante la distancia punto-recta?
La distancia punto-recta es importante porque nos permite determinar la distancia mínima entre un punto y una recta en el plano cartesiano. Esto es útil en diversas situaciones, como en problemas de optimización, seguridad o navegación.
2. ¿Cuáles son las fórmulas utilizadas para calcular la distancia punto-recta?
Para calcular la distancia punto-recta, utilizamos la fórmula de la distancia entre dos puntos para calcular la longitud del segmento que une el punto dado y el punto de intersección entre la recta perpendicular y la recta original.
3. ¿Podemos calcular la distancia punto-recta en diferentes dimensiones?
Sí, la distancia punto-recta puede ser calculada en diferentes dimensiones, como en el plano cartesiano bidimensional o en el espacio tridimensional. El procedimiento básico es el mismo, pero las fórmulas y ecuaciones pueden variar según la dimensionalidad del espacio.
4. ¿Qué sucede si el punto está en la recta?
Si el punto está en la recta, la distancia punto-recta será cero, ya que no hay necesidad de desplazarse desde el punto hacia la recta, ya que ya está en ella.
5. ¿Cómo podemos visualizar la distancia punto-recta en el plano cartesiano?
Podemos visualizar la distancia punto-recta trazando una línea perpendicular desde el punto hasta la recta en el plano cartesiano. La longitud de esta línea perpendicular corresponde a la distancia punto-recta.